Рассмотрим дифракцию Френеля на круглом отверстии. Если свет от точечного источника пропустить через малое отверстие, то на экране за отверстием наблюдается дифракционная картина. В случае использования монохроматического света, дифракционная картина имеет вид темных и светлых концентрических колец, например, в красном свете это будут концентрические черно-красные кольца. Кольца имеют радужную окраску, если применяется белый свет.
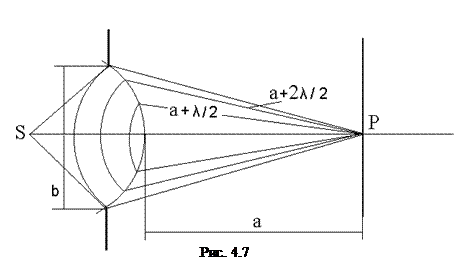
Пусть свет от точечного источника S падает на круглое отверстие диаметром b (рис. 4.7). Определим, какая будет интенсивность света на экране, находящемся на расстоянии a от отверстия, в центральной точке P. Для этого открытую часть сферической волновой поверхности разобьем на концентрические зоны (зоны Френеля), расстояния до которых от точки Р отличаются друг от друга на ![]() . Будем считать, что от каждой зоны в точку Р приходит одна волна. Следовательно, таким приемом число вторичных волн уменьшается до количества зон Френеля. Волны, пришедшие от соседних зон, имеют разность фаз, равную p, из-за существующей разности хода
. Будем считать, что от каждой зоны в точку Р приходит одна волна. Следовательно, таким приемом число вторичных волн уменьшается до количества зон Френеля. Волны, пришедшие от соседних зон, имеют разность фаз, равную p, из-за существующей разности хода ![]() и при наложении гасят друг друга.
и при наложении гасят друг друга.
 |
Таким образом, если в отверстии поместилось четное число зон Френеля, то в точке Р интенсивность света будет минимальной. При нечетном числе зон Френеля в этой точке образуется максимум интенсивности. Количество зон Френеля зависит от размера отверстия, расстояний от отверстия до источника и экрана, а также от длины волны падающего света. Интенсивность света в периферических точках будет периодически изменяться от минимума к максимуму. Чтобы убедиться в этом, нужно строить зоны Френеля для боковых точек, при таком построении на открытой части волновой поверхности зоны Френеля будут частично обрезаны. Интенсивность будет определяться соотношением площадей четных и нечетных зон Френеля, которое будет изменяться то в пользу четных, то нечетных по мере перемещения точки наблюдения из центра на периферию.