· Формула де Бройля:
а) в классическом приближении (V<<c, p=mV)
![]() ,
,
б) в релятивистском случае (V»c, 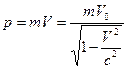 )
)
![]()
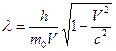 .
.
· Связь длины волны де Бройля с кинетической энергией Т частицы
а) в классическом приближении ![]() ;
;
б) в релятивистском случае ![]() ,
,
где Е0 – энергия покоя частицы (![]() ).
).
· Групповая скорость волн де Бройля
![]() .
.
где w — круговая частота; k- волновое число (![]() )
)
· Групповая скорость волн де Бройля
![]() .
.
· Соотношения де Бройля:
![]()
![]()
где Е – энергия движущейся частицы, р- импульс частицы, k – волновой вектор, ![]() =1,05×10-34 Дж×с – постоянная Планка.
=1,05×10-34 Дж×с – постоянная Планка.
· Соотношения неопределенностей:
а) для координаты и импульса частицы ![]() ,
,
б) для энергии и времени ![]() , где DЕ – неопределенность энергии данного квантового состояния; Dt – время пребывания системы в этом состоянии.
, где DЕ – неопределенность энергии данного квантового состояния; Dt – время пребывания системы в этом состоянии.
· Одномерное временное уравнение Шредингера для свободной частицы
![]() ,
,
где i – мнимая единица, m – масса частицы, Y(x,t) – волновая функция, описывающая состояние частицы.
Волновая функция, описывающая одномерное движение свободной частицы
![]() ,
,
где А – амплитуда волн де Бройля; рx =![]() - импульс частицы; Е=
- импульс частицы; Е=![]() — энергия частицы.
— энергия частицы.
· Одномерное уравнение Шредингера для стационарных состояний
![]() ,
,
где Е – полная энергия частицы; U(x) – потенциальная энергия; y(x) – волновая функция.
· Вероятность ![]() обнаружить частицу в интервале от x до x+dx (в одномерном случае)
обнаружить частицу в интервале от x до x+dx (в одномерном случае)
![]() ,
,
где![]() - плотность вероятности.
- плотность вероятности.
· Вероятность ![]() обнаружить частицу в интервале от x1 до x2 находится интегрированием
обнаружить частицу в интервале от x1 до x2 находится интегрированием ![]() в указанных пределах:
в указанных пределах:
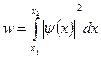 .
.
· Собственное значение энергии частицы En , находящейся на n-м энергетическом уровне в бесконечно глубокой прямоугольной потенциальной яме равно
![]() (n = 1, 2, 3,….)
(n = 1, 2, 3,….)
где l — ширина потенциальной ямы