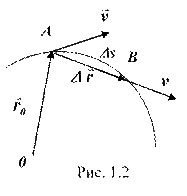
Пусть материальная точка двигается по какой-либо криволинейной траектории так, что в момент времени ![]() ей соответствует радиус-вектор
ей соответствует радиус-вектор ![]() (рис. 1.2). В течение малого промежутка времени
(рис. 1.2). В течение малого промежутка времени ![]() точка пройдет путь
точка пройдет путь ![]() и получит элементарное перемещение
и получит элементарное перемещение ![]() .Вектором средней скорости (<
.Вектором средней скорости (<![]() >) называется отношение приращения (
>) называется отношение приращения (![]() ) радиуса-вектора точки к промежутку времени (
) радиуса-вектора точки к промежутку времени (![]() ):
):
![]() .
.
![]() При неограниченном уменьшении
При неограниченном уменьшении ![]() средняя скорость стремится к предельному значению, которое называется мгновенной скоростью (
средняя скорость стремится к предельному значению, которое называется мгновенной скоростью (![]() ):
):
таким образом, мгновенная скорость есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. По мере уменьшения ![]() путь
путь ![]() все больше будет приближаться к
все больше будет приближаться к ![]() , поэтому
, поэтому
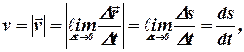
то есть модуль мгновенной скорости равен первой производной пути по времени.
При неравномерном движении модуль мгновенной скорости с течением времени изменяется. Поэтому пользуются скалярной величиной – средней скоростью неравномерного движения (![]() ):
):
![]() .
.
Длина пути, пройденного точкой за промежуток времени от ![]() до
до ![]() задается интегралом
задается интегралом ![]() .
.