Физическая величина, характеризующая быстроту изменения скорости по модулю и направлению, называется ускорением.
Средним ускорением неравномерного движения в интервале от ![]() до
до ![]() называется векторная величина, равная отношению изменения скорости (
называется векторная величина, равная отношению изменения скорости (![]() ) к интервалу времени (
) к интервалу времени (![]() ):
):
![]() .
.
Мгновенным ускорением (![]() ) материальной точки в момент времени
) материальной точки в момент времени ![]() будет предел среднего ускорения:
будет предел среднего ускорения:
![]()
Таким образом, ![]() есть векторная величина, равная первой производной скорости по времени.
есть векторная величина, равная первой производной скорости по времени.
При криволинейном движении скорость может меняться одновременно и по модулю, и по направлению. При этом движении полное ускорение равно: ![]() . Полное ускорение можно разложить на две составляющие: тангенциальное и нормальное ускорение.
. Полное ускорение можно разложить на две составляющие: тангенциальное и нормальное ускорение.
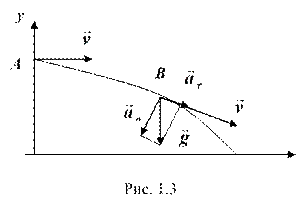
Например, при движении тела, брошенного горизонтально в поле тяжести Земли (рис. 1.3), тангенциальная составляющая ускорения равна первой производной по времени от модуля скорости, определяет быстроту изменения скорости по модулю:
![]() ;
;
нормальная составляющая ускорения равна:
![]()
направлена по нормали к траектории, к центру её кривизны и характеризует быстроту изменения скорости по направлению.
Полное ускорение тела равно геометрической сумме тангенциальной и нормальной составляющих:
![]() .
.
Для равномерного прямолинейного движения ![]() ,
, ![]() . При таком виде движения:
. При таком виде движения:
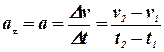 .
.
При ![]() и при
и при ![]() , получим:
, получим: ![]() . Проинтегрировав последнюю формулу, найдем, что длина пути равна:
. Проинтегрировав последнюю формулу, найдем, что длина пути равна:
![]()