Если на молекулы газа не действуют внешние силы, то молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в поле тяжести Земли. Два фактора – тяготение Земли и тепловое движение молекул – приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает.
Предполагая, что поле тяготения однородно (ускорение силы тяжести g=const), температура постоянна и масса всех молекул одинакова, можно получить формулу зависимости давления от высоты:
![]() (7.14)
(7.14)
Выражение (7.14) называется барометрической формулой. Здесь ![]() - давление на уровне моря,
- давление на уровне моря, ![]() – давление на высоте
– давление на высоте ![]() над уровнем моря.
над уровнем моря.
График зависимости ![]() изображен на рис. 7.6. Из графика видно, что давление очень быстро убывает с высотой:
изображен на рис. 7.6. Из графика видно, что давление очень быстро убывает с высотой:
![]() ;
; ![]() .
.
Уже на высоте ![]() =12 км давление составляет четвертую часть от нормального. Барометрическую формулу можно преобразовать, если воспользоваться выражением
=12 км давление составляет четвертую часть от нормального. Барометрическую формулу можно преобразовать, если воспользоваться выражением ![]() :
:
![]() (7.15)
(7.15)
Если учесть, что 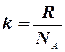 , а
, а 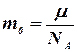 , то формулы (7.14) и (7.15) приобретают вид:
, то формулы (7.14) и (7.15) приобретают вид:
![]() .
.
Выражение (7.15) называется распределением Больцмана во внешнем потенциальном поле. Из него следует, что концентрация молекул, а, следовательно, плотность газа, больше там, где меньше потенциальная энергия его молекул.
Для частиц одинаковой массы, находящихся в состоянии хаотического теплового движения, распределение Больцмана справедливо не только в поле тяжести, но в любом внешнем потенциальном поле.