Финансовый актив можно охарактеризовать по цене, стоимости, доходности и риску. Принятие инвестором решения о приобретении того или иного актива может опираться на абсолютные, либо на относительные показатели. В первом случае речь может идти о цене и (или) стоимости актива, во втором – о его доходности.
Финансовый актив имеет две взаимосвязанные абсолютные характеристики: во-первых, объявленную текущую рыночную цену (Рm), по которой его можно приобрести на рынке, и, во-вторых, теоретическую, или внутреннюю, стоимость (Vt).
В зависимости оттого, что является методологическим и информационным обеспечением процесса оценивания, существуют три основные теории оценки: фундаменталистская, технократическая и теория «ходьбы наугад» (рис. 2.5).
При фундаменталистском подходе оценки финансовых активов считается, что каждый финансовый актив имеет внутреннюю стоимость или ценность, которая может быть количественно оценена как дисконтированная стоимость будущих денежных поступлений, генерируемых этим финансовым активом.
Если фундаменталисты предполагают двигаться от будущего к настоящему, то технократы наоборот, от прошлого к настоящему. Они утверждают, что внутреннюю стоимость конкретного финансового актива можно рассчитать, зная динамику его цен в прошлом.
Согласно способу «ходьба наугад» стоимость финансового актива (его цена) отражает всю информацию, в том числе и относительно будущего данного финансового актива, то есть никакой другой информации о текущей стоимости финансового актива не требуется.
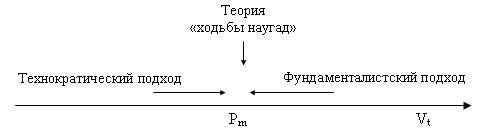
Рис. 2.5 Теории оценки финансовых активов
На сегодняшний день общепризнанным считается фундаменталистский подход к оценке финансового актива, согласно которому внутренняя стоимость финансового актива определяется по формуле:
![]() , (2.6)
, (2.6)
где i – период; CFi – ожидаемые денежные поступления в конкретном i-м периоде; n – ставка по депозитам, которую предлагает банк в текущем периоде (банковский процент).
Доходность финансового актива в конкретный интервал времени t обозначим E(rt). Ожидаемую доходность актива можно определить по формуле (формуле среднего арифметического):
 , (2.7)
, (2.7)
где N – количество раз наблюдений за доходностью конкретного финансового актива; ![]() – ожидаемое значение доходности в конце t-го холдингового периода.
– ожидаемое значение доходности в конце t-го холдингового периода.
Если учесть, что конкретная цена финансового актива получена с некоторой долей вероятности (Pt), то ожидаемую доходность финансового актива можно рассчитать по формуле:
![]() . (2.8)
. (2.8)
Пример 1
Инвестор пытается оценить различные варианты изменения экономической ситуации:
А) Pt = 0,10; rt = 0,08;
Б) Pt = 0,15; rt = 0,12;
В) Pt = 0,25; rt = 0,15.
Определим доходность финансового актива:
Е(rt) = (0,1 * 0,08) + (0,15 * 0,12) + (0,25 * 0,15) = 0,0635 = 6,3 %.
Риск вложения в финансовый актив можно определить как степень несовпадения реальной доходности финансового актива с ожидаемой доходностью. Чем больше будет это несовпадение, тем больше будет риск.
Количественно риск вложения в ценную бумагу можно оценить с помощью следующих показателей:
1) среднеквадратического (стандартного) отклонения:
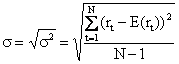 . (2.9)
. (2.9)
Стандартное отклонение характеризует колеблемость результата. Чем больше стандартное отклонение, тем больше риск вложения в данный финансовый актив;
2) коэффициента вариации:
![]() . (2.10)
. (2.10)
Если ν < 10 %, то колеблемость считается низкой; если 10 % < ν < 25 %, то колеблемость считается умеренной; если ν > 25 %, то колеблемость высокая.
Пример 2
Наблюдали за ценой акций в течение определённого времени. Длительность холдингового периода 1 месяц.
|
Дата: |
09.06 |
09.07 |
09.08 |
09.09 |
09.10 |
|
Цена: |
16,2 |
17,01 |
18,71 |
18,15 |
19,42 |
Определить стандартное отклонение и коэффициент вариации.
Решение:
1) Определим ожидаемую доходность финансового актива:
![]()
2) Определим среднеквадратическое отклонение:
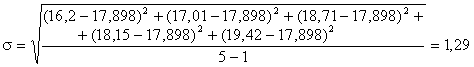 .
.
1) Определим коэффициент вариации:
![]() .
.
Ответ: ν < 10 %, это означает, что колеблемость результата слабая.