Принятие управленческих решений инвестиционного характера базируется на сравнении объемов предполагаемых инвестиций и будущих денежных поступлений от реализации инвестиционных проектов. Существуют различные методы и критерии оценки эффективности инвестиционных проектов, например:
1) метод расчета чистого приведенного эффекта (или метод расчета чистой текущей стоимости);
2) метод расчета индекса рентабельности инвестиции;
3) метод расчета внутренней нормы прибыли инвестиций (внутренний коэффициент эффективности): IRR;
4) метод определения срока окупаемости;
5) метод расчета коэффициента эффективности (учетная норма прибыли);
6) анализ инвестиционных проектов в условиях инфляции;
7) метод расчета чистого приведенного эффекта (или метод расчета чистой текущей стоимости).
Метод расчета чистого приведенного эффекта (или метод расчета чистой текущей стоимости) основан на сравнении величины исходной инвестиции (IC) с суммой дисконтированных чистых денежных поступлений, которые генерируются этой инвестицией в течение прогнозируемого интервала времени:
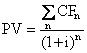 ; (2.14)
; (2.14)
![]() ; (2.15)
; (2.15)
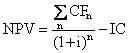 ; (2.16)
; (2.16)
где i – ставка начисления; n – период начисления.
При оценке чистой текущей стоимости возможны три варианта:
1) NPV > 0 – в этом случае инвестор получает прибыль за весь срок реализации проекта; инвестиционный проект принимается инвестором;
2) NPV < 0 – проект убыточен и не позволяет вернуть даже вложенные средства;
3) NPV = 0 – данный проект безубыточен, не приносит убытков, но и прибыли тоже.
Метод расчета индекса рентабельности инвестиции предполагает определение индекса рентабельности инвестиции по следующей формуле:
![]() . (2.17)
. (2.17)
Если PI > 1, то проект следует принять, если PI < 1, то проект отвергается, если PI = 1, то проект является ни прибыльным, ни убыточным.
В отличие от чистой текущей стоимости, индекс рентабельности является относительной величиной. Он характеризует уровень дохода на единицу затрат, то есть характеризует эффективность вложений. Чем больше этот показатель, тем выше отдача каждого рубля, вложенного в инвестиционный проект.
Критерий «рентабельности инвестиций» очень удобен при выборе одного проекта из ряда альтернативных, имеющих примерно одинаковое значение чистой текущей стоимости (NPVn). Например, если два проекта имеют одинаковые значения NPVn, но
разные объемы требуемых инвестиций, то выгоднее будет тот, который обеспечивает наибольшую эффективность проекта.
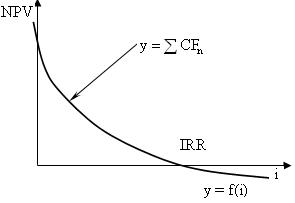
Рис. 2.7. Изменение чистой текущей стоимости классического инвестиционного проекта
При методе расчета внутренней нормы прибыли инвестиций (внутренний коэффициент эффективности) внутренний коэффициент эффективности (IRR) находится как значение рентабельности, при котором чистая текущая стоимость, рассчитанная с нарастающим итогом равным нулю:
IRR = i, если NPVn = 0 (2.18)
где i– банковский процент.
Внутренний коэффициент эффективности (IRR) можно рассчитать по формуле для расчета чистой текущей стоимости, вместо показателя i подставив IRR:
![]() . (2.19)
. (2.19)
Уравнение (2.19) решается методом линейно-кусочной аппроксимации, либо с помощью электронных таблиц Excel.
Правило внутренней нормы доходности: принимать необходимо те проекты, у которых ставка дисконта меньше внутренней нормы доходности (i < IRR). Если i = IRR, то проект ни прибыльный ни убыточный.
Метод определения срока окупаемости является одним из самых простых и широко распространенных в мировой практике. Если доход распределяется по годам равномерно, то срок окупаемости рассчитывается делением затрат на величину годового дохода, который обусловлен этими затратами.
Если прибыль распределяется равномерно по годам, то срок окупаемости (Т) рассчитывается прямым подсчетом числа лет, в течение которых инвестиция будет погашена, либо кумулятивным денежным потоком (срок окупаемости без учета фактора времени), либо чистой текущей стоимостью, рассчитанной с нарастающим итогом (срок окупаемости с учетом фактора времени).
Общая формула расчета срока окупаемости (Т) имеет вид:
![]() Т = nmin, при котором
Т = nmin, при котором ![]() .
.
Нередко показатель Т рассчитывается более точно, т.е. рассматривается и дробная часть года; при этом делается молчаливое предположение, что денежные потоки распределены равномерно в течение каждого года. Так, для проекта с денежным потоком (млн. р.) – 100, 40, 40, 40, 30, 20 значение показателя Т равно 3 годам, если расчет ведется с точностью до целого года, или 2,5 года в случае точного расчета.
Коэффициента эффективности (учетная норма прибыли) рассчитывается делением средней годовой прибыли на среднюю величину инвестиций:
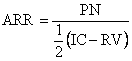 , (2.20)
, (2.20)
где PN – средняя годовая прибыль; RV – ликвидационная стоимость объекта инвестиций.
Так как в условиях инфляции резко возрастают риски, при оценке инвестиционных проектов проводится анализ инвестиционных проектов. Для того чтобы учесть данные риски, строят имитационную модель учета риска.
Данная модель связана с корректировкой денежного потока и последующими расчетами NPV для всех возможных вариантов. Методика анализа имитационной модели учета риска такова:
1) по каждому из рассматриваемых проектов строятся три различных варианта развития событий (пессимистический, наиболее вероятный, оптимистический);
2) у каждого из вариантов рассчитывается соответствующая чистая текущая стоимость:
- пессимистическая (NPVn);
- наиболее вероятная (NPVнВ);
- оптимистическая (NPV0);
3) для каждого из вариантов проектов рассчитывается размах вариации NPV:
R (NPV) = NPV0 – NPVn; (2.21)
4) из рассматриваемых проектов тот считается наиболее рискованным, у которого размах вариации больше.