Использование интегрального способа позволяет получать более точные результаты расчета влияния факторов по сравнению со способами цепной подстановки, абсолютных и относительных разниц, поскольку дополнительный прирост результативного показателя от взаимодействия факторов присоединяется не к значению последнего фактора, а делится поровну между значениями всех факторов.

Рассмотрим алгоритмы расчетов влияния факторов для разных моделей.

Для мультипликативной двухфакторной модели

У = q * p

алгоритм следующий:

;

.

Рассмотрим данную методику на примере (табл. 14.5):

;

Таблица 14.5 Исходные данные для анализа влияния факторов на объем выпуска продукции интегральным способом

Для мультипликативной трехфакторной модели

f = x * y * z

алгоритм следующий:

;

;

.

Для мультипликативной четырехфакторной модели

f = x * y * z * q

алгоритм следующий:

Рассмотрим, как рассчитывается влияние факторов в кратных и смешанных моделях.

Для факторной модели вида

используются следующие формулы:

;

.

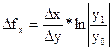Для факторной модели вида

используются следующие формулы:

;

;

.
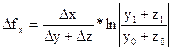