Метод восходящего синтаксического анализа (снизу вверх) состоит в том, что отталкиваясь от заданной цепочки пытаются привести ее к начальному символу (аксиоме грамматики), т.е. восходя от листьев, построить дерево син­таксического анализа.

Рассмотрим общие принципы работы детерминированного восходящего синтаксического анализатора. Для заданной входной цепочки восходящий МП-автомат моделирует ее правый вывод в обратном порядке, т.е. правила грамма­тики применяются справа налево, и манипулирует своими магазинными и текущими входными символами с помощью операций переноса и свертки.

Операция переноса — это операция, которая вталкивает в магазин некото­рый символ, соответствующий текущему входному символу и сдвигает вход, т.е. переносит со входа в магазин текущий символ.

Операция свертки, для некоторого правила р с r символами в правой части — это операция, которая выбирается только тогда, когда r верхних символов мага­зина представляют правую часть правила р. Операция свертки выталкивает из магазина верхние r символов и вталкивает туда символ, соответствующий левой части правила р.

Пример 3.4.1. Пусть задана грамматика G = <N, T, P, S>, у которой

N = <S, L, I>, T = {i, , , real}, S = {S},

P = {      1. S real L

              2. L L, I

              3. L I

              4. I  i }

и входная цепочка real i, i.

Правый вывод этой цепочки в грамматике G имеет вид:

    _{1             2                 4                3               4}

Sreal Lreal L, Ireal L, ireal I, ireal i, i

Прослеживание полученного правого вывода в обратном порядке можно интерпретировать как построение дерева вывода.

При этом на каждом шаге вхождение правой части некоторого правила за­меняется нетерминалом из левой части этого правила (рис. 3.6).

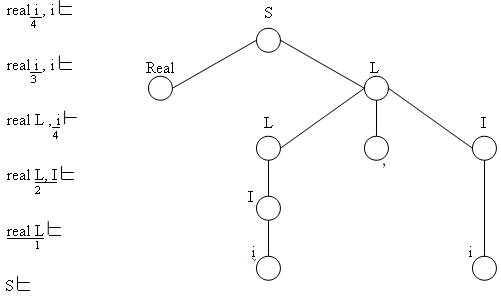
Рис. 3.6. Обращение правого вывода примера 3.4.1

Каждую подчеркнутую подцепочку называют «основой» цепочки, в кото­рой она встречается.

Основа цепочки, состоящей из терминалов и нетерминалов, — это вхожде­ние правой части последнего правила, примененного в правом выводе этой цепочки.

При моделировании обратного правого вывода с помощью МП-автомата осуществляется ПЕРЕНОС входных символов из входной ленты в магазинную память до тех пор, пока на верхушке магазина не окажется основа цепочки, к кото­рой затем и применяется операция СВЕРТКА, которая выполняет замену ос­новы левой частью соответствующего правила.

Для приведенного выше примера правого вывода цепочки real i, i  работа МП-автомата, моделирующего этот вывод, может быть описана в виде следующей последовательности конфигураций и выполняемых при этом ко­манд МП-автомата:

Анализ данного описания показывает, что конкатенация содержимого ма­газина и входной ленты МП-автомата в каждом такте его работы однозначно соответствует промежуточным цепочкам, получаемым на соответствующих шагах правого вывода в КС-грамматике. При этом в силу того, что автомат является детерминированным, комбинация входного символа на ленте и сим­вола на вершине магазина должны в

каждом такте работы МП-автомата од­нозначно инициировать выполнение одной из его команд: ПЕРЕНОС, ОТВЕРГНУТЬ, ДОПУСТИТЬ, или СВЕРТКА (k), где k — номер основываю­щей подстановки. Для нашего примера комбинация символа «i» в магазине и символа «,» или символа « » во входной строке инициируют операцию МП-автомата СВЕРТКА (4).

Возникает естественный вопрос: для любой ли КС-грамматики можно най­ти такие комбинации, если нет, то какими свойствами должна обладать КС- грамматика, чтобы это сделать и каким образом. К сожалению, общей процедуры, дающей ответ на поставленный вопрос, нет. И для каждой конк­ретной грамматики требуется более тонкий анализ ее правил, а то и струк­туры возможных в ней выводов. Существуют различные подходы к проведению такого анализа и, соответственно, построению управляющей таблицы МП-автомата.

Наиболее универсальный из них — это метод Кнута (LR(k)-метод) [9]. На­звание LR(k) означает, что детерминированный синтаксический анализатор читает входную цепочку слева (Left) и выдает ее правый (Right) анализ на ос­нове уже прочитанной части входной цепочки (левый контекст) и фиксирован­ного числа предварительно просматриваемых символов (максимум k). В принципе, любая из однозначных КС-грамматик может рассматриваться как LR(k)-грамматика, при этом k = 0, 1, …, n.

Однако на практике LR(k)-метод не получил широкого распростране­ния из-за своей громоздкости. К тому же было доказано, что если для опи­сания процесса порождения предложений некоторого языка построена КС-грамматика, которая является LR(k)-грамматикой, то этот же язык мо­жет порождаться и LR(1)-грамматикой (другое дело как построить эту грам­матику!). Другими словами, все детерминировано разбираемые КС-языки могут разбираться LR(1)-методом, и в случае восходящего разбора увели­чение k-числа предварительно просматриваемых символов не ведет к воз­можности детерминированного анализа большего числа языков. Это совершенно не похоже на LL методы разбора (детерминированный разбор сверху вниз), там LL(k) метод позволяет разобрать более широкий класс языков, чем например, LL(1) метод.

Оказалось также, что для описания синтаксиса языков программирова­ния [9] бывает достаточно не только LR(1)-грамматик, а даже, так называемых, SLR(1)-грамматик. SLR(1)-грамматика — простая (simple) LR(l)-грамматика. SLR(l)-грамматика отличается от LR(l)-грамматик тем, что для определения конца основы в SLR(l)-грамматике используется только один предварительно просмотренный символ (как и в LR(1)), но никакого внимания не уделяется левому контексту (т.е. не учитывается уже обработанная часть цепочки), тогда как в более общем случае LR(1) метода левый контекст учитывается и даже играет решающую роль. Еще раз напомним, что речь идет не об описании ра­боты МП-автомата, а о построении его управляющих таблиц, т.е. этапе анали­за правил грамматики.

Существуют и другие подходы к построению детерминированного вос­ходящего МП-автомата, но они применимы к более узким классам КС-грамма­тик. Наиболее известный из них — метод предшествования, применим он к так называемым грамматикам простого предшествования.

С позиций универсальности применения различных методов к построе­нию детерминированного восходящего синтаксического анализатора для раз­личных классов КС-грамматик, эти грамматики образуют иерархию грамматик. Эта иерархия показана на рис.3.7.

Детерминированные однозначные КС-языки

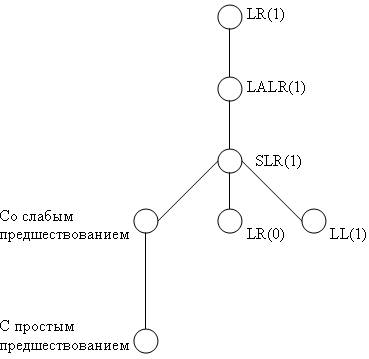
Рис 3.7. Иерархия грамматик

Не существует общей процедуры, которая бы могла определить, к какому классу относится та или иная КС-грамматика. Нельзя, например, решить, существует ли такое значение k, для которого заданная грамматика будет LR(k)-грамматикой. Но можно определить, обладает ли конкретная грам­матика признаком LR(k) для заданного k. В частности, можно решить, явля­ется ли грамматика LR(0) или LR(1)-грамматикой. Либо можно выяснить, является ли данная КС-грамматика грамматикой простого предшествова­ния и т.д. Выяснить это можно лишь путем применения конкретного метода построения синтаксического анализатора, т.е. например, если применяется метод предшествования, и в результате его применения построен анализа­тор по методу предшествования, то можно утверждать, что исходная КС-грамматика является грамматикой предшествования. Иерархия грамматик, показанная на рис. 3.6, отражает и сложность построения анализаторов того или иного типа. Более просто это выполняется для грамматик нижних уровней и менее тривиально для LR(1)-грамматик. Поэтому на практике обычно стараются воспользоваться менее сложным методом и лишь при неуспехе переходить к более универсальным. Эта стратегия применяется и в автоматических генераторах синтаксических анализаторов [9].