Определение 4.3.1. [10] Атрибутной формальной грамматикой (А-грамматикой) называется пара
![]()
Здесь G = <N, T, P, S> – безатрибутная КС-грамматика; А – атрибутная компонента,
![]()
где Х – множество атрибутов;
![]() 1,
1,![]() p – множество функций и предикатов, заданных на множестве Х со значениями во множестве R.
p – множество функций и предикатов, заданных на множестве Х со значениями во множестве R.
Каждому символу ![]()
![]() T
T![]() N сопоставлено два непересекающихся множества:
N сопоставлено два непересекающихся множества:
· множество унаследованных атрибутов Ху(![]() );
);
· множество синтезированных атрибутов Хс(![]() ).
).
При этом выполняются условия ![]() X(
X(![]() ) = X, Xy(
) = X, Xy(![]() )
)![]() Xc(
Xc(![]() ) =
) =![]() , X(
, X(![]() )=Xy(
)=Xy(![]() )
)![]() Xc(
Xc(![]() ).
).
Правила вычисления атрибутов определяется следующим образом [17]:
а) начальное значение каждого унаследованного атрибута для начального символа грамматики S (аксиомы) задается;
б) каждому вхождению унаследованного атрибута X символа в правой части правила подстановки сопоставляется правило вычисления значения этого атрибута как функции (предиката) от некоторых других атрибутов символов, входящих в правую или левую части данной подстановки;
в) каждому вхождению синтезированного атрибута X нетерминального символа, входящего в правую или левую часть подстановки, ставится в соответствие правило вычисления как функции (предиката) других атрибутов символов, входящих в левую или правую части подстановки.
Атрибутная грамматика связывает атрибуты с вершинами синтаксического дерева вывода. Семантические правила вычисления значений атрибутов, соответствующие правилу КС-грамматики, применяются для всех вхождений этого правила в дерево вывода. Синтезированные атрибуты некоторой вершины хранят информацию, которая синтезируется из поддерева этой вершины и передается вверх к корню дерева. Унаследованные атрибуты служат для хранения информации, которая передается сверху вниз, от корня дерева к его листьям. Фактически унаследованные атрибуты определяют контекст, в котором погружена вершина вместе со своим поддеревом. Контекстно-зависимые условия входного языка должны выражаться через ряд условий, входящих в семантические правила А-грамматики. Наконец, эти условия должны
выражать соотношения между значениями атрибутов, которые выполняются в дереве вывода правильной программы.
Описание семантики языка с помощью атрибутных грамматик позволяет определить «смысл» исходной программы, как значения одного или нескольких специальных атрибутов корня синтаксического дерева этой программы. Поскольку главной задачей в процессе трансляции является получение объектной программы, то можно считать, что один из специальных атрибутов корня синтаксического дерева получает значение — последовательности операций абстрактной машины, т.е. объектную программу.
Определение 4.3.2. [17]. Атрибутной трансляционной грамматикой (АТ-грамматикой) называется трансляционная грамматика, к которой добавлены атрибуты и семантические правила их вычисления для нетерминальных, терминальных и операционных символов (символов действий).
Правила вычисления значений атрибутов для нетерминальных и терминальных вершин дерева вывода аналогичны правилам, указанным в определении 4.3.1. Для вычисления значений атрибутов символов действий вводится дополнительное правило:
· каждому синтезированному атрибуту символа действия сопоставляется правило вычисления значения этого атрибута как функции (предиката) некоторых других атрибутов символов действий.
Таким образом, в АТ-грамматике терминальные, нетерминальные и операционные символы должны быть атрибутными. Каждый атрибут нетерминального или операционного символов задается либо как синтезируемый, либо как наследуемый. Значения атрибутов входных (терминальных символов) задаются.
Для записи правил АТ-грамматики приняты следующие соглашения:
1) Имена атрибутов используются в качестве переменных и записываются в виде индексов у соответствующих символов грамматики.
2) Семантические правила вычисления значений атрибутов записываются под каждой продукцией в форме оператора присваивания, при этом вместо «=» используется знак «![]() ». В правой части от «
». В правой части от «![]() » стоит либо выражение, либо имя процедуры (функции), с помощью которой и осуществляется вычисление значения атрибута. В левой части — имя переменной (атрибута) или их список, которым присваивается значение, вычисленное в правой части правила.
» стоит либо выражение, либо имя процедуры (функции), с помощью которой и осуществляется вычисление значения атрибута. В левой части — имя переменной (атрибута) или их список, которым присваивается значение, вычисленное в правой части правила.
3) Имена переменных для каждого правила подстановки являются локальными и не зависят от имен переменных (атрибутов) в других правилах грамматики.
Например, если нетерминал X имеет два синтезируемых и один наследуемый атрибуты, а нетерминалы Y и Z по одному наследуемому и одному синтезируемому атрибуту, а терминал b — один атрибут, то правило
X![]() bYZ {ПЕЧАТЬ},
bYZ {ПЕЧАТЬ},
где {ПЕЧАТЬ} — операционный символ, в АТ-грамматике будет иметь вид:
Xp, q, r![]() bsYy,u Zv,w {ПЕЧАТЬ}m.
bsYy,u Zv,w {ПЕЧАТЬ}m.
Если q, р — синтезируемые, а у, v, m, p — наследуемые атрибуты, то правила их вычисления могут быть заданы, например, в виде:
q![]() SIN(n+w);
SIN(n+w);
(r, w) ![]() S*n;
S*n;
y![]() p;
p;
m![]() p.
p.
Определение 4.3.3.[17]. Атрибутная грамматика, в которой любое дерево вывода завершенное, называется корректной.
Среди грамматик, используемых для описания языков программирования, особое место занимают так называемые L-атрибутные грамматики. Этот класс грамматик допускает построение синтаксических анализаторов (атрибутных МП-автоматов), которые решают задачи о принадлежности той или иной цепочки терминальных символов, снабженных атрибутами, языку, порождаемому заданной атрибутной грамматикой.
Определение 4.3.4. [17] Атрибутная трансляционная грамматика называется L-атрибутной тогда и только тогда, когда выполняются следующие три условия
1) в каждом правиле вычисления значения унаследованного атрибута некоторого символа из правой части подстановки, каждый аргумент этого правила представляет собой унаследованный атрибут некоторого символа, стоящего в правой части подстановки левее рассматриваемого символа;
2) в каждом правиле вычисления значения синтезированного атрибута символа, стоящего в левой части подстановки, любой аргумент этого правила — это или унаследованный атрибут этого символа, или произвольный атрибут символа из правой части данной подстановки;
3) в каждом правиле вычисления значения атрибута символа, соответствующего синтезируемому атрибуту символа действия, любой аргумент этого правила — наследуемый атрибут данного символа действия.
Свойства L-атрибутности (L в данном случае — это сокращение, Left — левый) накладывает дополнительные ограничения на правила вычисления унаследованных и синтезированных атрибутов. Суть ограничений состоит в том, что унаследованные атрибуты данного символа зависят от информации, которая находится слева от него. Вводимые же ограничения вычисления значений синтезированных атрибутов (условия 2 и 3) исключают круговую зависимость атрибутов.
Таким образом, если дана продукция грамматики А![]() ВС, где А, В, С
ВС, где А, В, С![]() N, то атрибуты символов А, В, С должны вычисляться в следующем порядке:
N, то атрибуты символов А, В, С должны вычисляться в следующем порядке:
1) унаследованные атрибуты А;
2) унаследованные атрибуты В;
3) синтезированные атрибуты В;
4) унаследованные атрибуты С;
5) синтезированные атрибуты С;
6) синтезированные атрибуты А.
Этот порядок соответствует обходу синтаксического дерева сверху вниз и слева направо: «спускаясь» вниз от вершины, вычисляем унаследованные атрибуты, «поднимаясь» вверх к вершине, вычисляем синтезированные атрибуты.
Пример 4.3.1. [17]. Покажем, как можно применять АТ-грамматику при построении компилятора на примере трансляции оператора присваивания некоторого гипотетического языка программирования.
Пусть синтаксис оператора присваивания задается с помощью следующей КС-грамматики G = <М, Т, Р, S>, где
N = {S, E, K, P, R, L},
T = {(, ), *, +, i, :=};
S = {S};
P = {S![]() i:= E
i:= E
E![]() KR
KR
R![]() + KR
+ KR
![]()
K![]() PL
PL
L![]() *PL
*PL
![]()
P![]() i
i
p![]() (E)}
(E)}
Данная грамматика порождает операторы присваивания, в правой части которых стоит арифметическое выражение, в состав которого входят операции * и +. Символ i обозначает идентификатор и снабжается целочисленным индексом — указателем на соответствующий элемент таблицы идентификаторов. Так оператор присваивания вида
r:=(b + c)*d
в этом случае записывается следующим образом
i1:=(i2+i3)*i4
и ему соответствует дерево разбора на рис. 4.9.
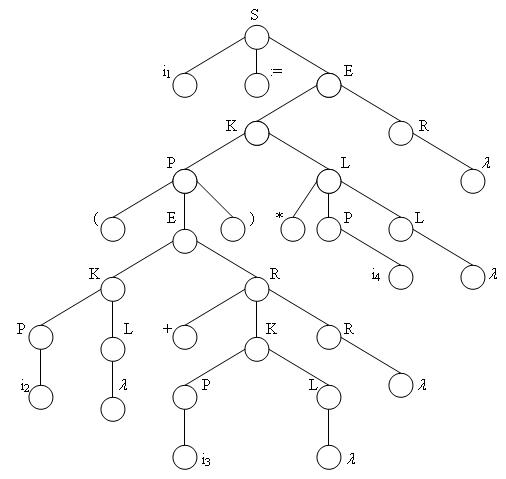
Рис. 4.9. Синтаксическое дерево разбора цепочки i1:= (i2+i3)*i4
После трансляции данной цепочки должна быть получена программа, отражающая последовательность операций абстрактной машины при выполнении данного оператора присваивания:
{СЛОЖИТЬ}2, 3, 200 {УМНОЖИТЬ}200, 4, 201 {ПРИСВОИТЬ}1, 201
Здесь {СЛОЖИТЬ}, {УМНОЖИТЬ}, {ПРИСВОИТЬ} — имена действий абстрактной машины (процедур), реализация которых обеспечивает выполнение соответствующего оператора присваивания. Индексы при действиях – это указатели на адреса памяти, в которых хранятся (или куда помещаются) значения операндов соответствующих операций.
Таким образом, наша задача состоит в том, чтобы средствами АТ-грамматики описать процесс перевода оператора присваивания в последовательность действий абстрактной машины. Для этой цели сначала по исходной КС-грамматике построим трансляционную грамматику цепочечного перевода. Правила Т-грамматики примут вид:
S![]() i:= E{ПРИСВОИТЬ}
i:= E{ПРИСВОИТЬ}
E![]() KR
KR
R![]() +K{СЛОЖИТЬ} R
+K{СЛОЖИТЬ} R
![]()
K![]() PL
PL
P![]() *P{УМНОЖИТЬ} L
*P{УМНОЖИТЬ} L
![]()
P![]() i
i
P![]() (E)
(E)
Для того чтобы эта грамматика стала атрибутной, зададим теперь атрибуты и правила их вычисления.
Операционные символы {СЛОЖИТЬ} и {УМНОЖИТЬ} будут иметь по три, а {ПРИСВОИТЬ} — два унаследованных атрибута. Значениями атрибутов символов {СЛОЖИТЬ} и {УМНОЖИТЬ} являются указатели на позиции таблицы, в которых хранятся значения левого, правого операндов и результата соответственно. Значения атрибутов символа {ПРИСВОИТЬ} — указатели на позиции таблицы, соответствующие идентификатору левой части оператора присваивания и значению выражения, стоящего в его правой части.
У нетерминала S атрибутов нет. Нетерминалы Е, К, Р имеют по одному синтезированному атрибуту, значением этого атрибута является указатель на элемент таблицы, содержащий результат вычисления подвыражения, порожденного соответствующим нетерминалом. Нетерминалы R и L имеют по два атрибута, первый из которых является унаследованным, а второй — синтезированным.
Терминальный входной символ i снабжается численным атрибутом, значение которого — указатель на позицию таблицы, хранящей значение идентификатора.
Будем полагать, что для вычисления значений синтезированных атрибутов используется процедура НОВТ без параметров, выдающая в качестве значения указатель на незанятую позицию таблицы идентификаторов.
Атрибутная грамматика, снабженная комментариями об атрибутах символов, имеет следующий вид:
Ex – СИНТЕЗИРУЕМЫЙ х
Кх – СИНТЕЗИРУЕМЫЙ х
Pх – СИНТЕЗИРУЕМЫЙ х
Rx,y – УНАСЛЕДОВАННЫЙ x, СИНТЕЗИРУЕМЫЙ y
Lx,y – УНАСЛЕДОВАННЫЙ х, СИНТЕЗИРУЕМЫЙ y
{СЛОЖИТЬ}x, y, z – УНАСЛЕДОВАННЫЕ х, у, z
{УМНОЖИТЬ}x, y, z – УНАСЛЕДОВАННЫЕ х, у, z
{ПРИСВОИТЬ}x, y – УНАСЛЕДОВАННЫЕ х, у
1) S![]() ia1:=Eb1 {ПРИСВОИТЬ}a2, b2
ia1:=Eb1 {ПРИСВОИТЬ}a2, b2
a2![]() a1 b2
a1 b2![]() b1
b1
2) Eb2![]() Ka1Ra2, b1
Ka1Ra2, b1
a2![]() a1 b2
a1 b2![]() b1
b1
3) Ra1, b2![]() +Kb1{СЛОЖИТЬ}a2, b2, c1 Rc2, d1
+Kb1{СЛОЖИТЬ}a2, b2, c1 Rc2, d1
a2![]() a1 c2
a1 c2![]() c1
c1
b2![]() b1 d2
b1 d2![]() d1
d1
c1![]() НОВТ
НОВТ
4) ![]()
a2![]() a1
a1
5) Kb2![]() Pa1La2, b1
Pa1La2, b1
a2![]() a1 b2
a1 b2![]() b1
b1
6) La1, d2![]() *Kb1{УМНОЖИТЬ} a2, b2, c1 Lc2d1
*Kb1{УМНОЖИТЬ} a2, b2, c1 Lc2d1
a2![]() a1 c2
a1 c2![]() c1
c1
b2![]() b1 d2
b1 d2![]() d1
d1
c1![]() НОВТ
НОВТ
7) ![]()
a2![]() a1
a1
8) Pa2![]() ia1
ia1
a2![]() a1
a1
9) Pa2![]() (Ea1)
(Ea1)
a2![]() a1
a1
Предположим, что процедура НОВТ при обращении к ней выдает последовательные адреса ячеек памяти, начиная с адреса 200. Тогда входная последовательность i1 := (i2 + i3) * i4 имеет атрибутное дерево вывода, показанное на рис. 4.10.
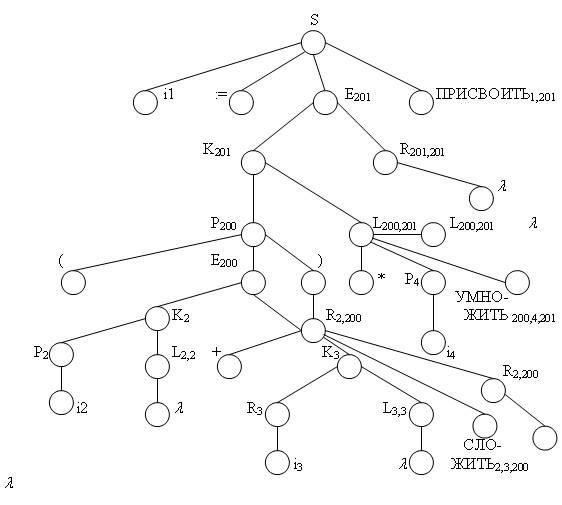
Рис. 4.10. Атрибутное дерево вывода входной последовательности i1 := (i2 + i3) * i4
Активная цепочка имеет вид:
i1:=(i2+i3{СЛОЖИТЬ}2, 3, 200)*i4{УМНОЖИТЬ}200, 4, 201{ПРИСВОИТЬ}1, 201
а операционная ее часть выглядит следующим образом:
{СЛОЖИТЬ}2, 3, 200 {УМНОЖИТЬ}200, 4, 201 {ПРИСВОИТЬ}1, 201
и по ней уже достаточно просто сгенерировать последовательность команд объектной машины для вычисления значения исходного выражения.