Страховая статистика находит широкое применение в актуарных расчетах. Она фиксирует, систематизирует и изу­чает показатели наиболее типичных, массовых явлений в страховании и их изменение во времени (так называемые, динамические ряды показателей).

Статистика с помощью наблюдения фактов и обстоя­тельств наступления тех или иных страховых случаев в про­шлом получает данные для прогнозирования статистичес­кой вероятности страхового риска. Анализ полученной информации служит целям предвидения будущего размера ущерба. Чем больше число объектов наблюдения, тем дос­товернее основа для оценки будущего развития событий.

Для определения расчетных показателей страховой ста­тистики используют следующие исходные данные (в скобках даны иные обозначения, иногда приводимые в некоторых учебно-методических разработках):

1) число объектов страхования – n (N, a);   

2) страховая сумма для любого объекта страхования – SSn (S, b);

3) число страховых событий – е (L, c);

4) число пострадавших объектов в результате страховых со­бытий – т (M, d);

5) сумма выплаченного страхового возмещения – SQ (f);

6) сумма собранных страховых платежей – Sp;

7) страховая сумма, приходящаяся на поврежденный объект наблюдаемой совокупности – SSm.

Дадим краткую характеристику расчетным показателям страховой статистики.

Частота страховых событий:

          Чс < 1.

Частота страховых событий показывает, сколько стра­ховых случаев приходится на один объект страхования. Дан­ное соотношение может быть представлено количественно как величина меньше единицы. Это означает, что одно страховое событие может повлечь за собой несколько стра­ховых случаев. Отсюда следует различать понятия « страховой случай» и «страховое событие». Страховым событием могут быть град, эпидемия и т.п., влияющие своим воздействием на многие объекты страхования (страховые случаи).

Опустошительность страхового события, коэффици­ент кумуляции риска:

            

Коэффициент кумуляции риска показывает, сколько застрахованных объектов застигает то или иное событие, иначе говоря, сколько страховых случаев может состояться. Минимальный коэффициент кумуляции риска равен еди­нице. Если опустошительность больше единицы, то будет больше кумуляция риска и больше численное различие между числом страховых событий и числом страховых слу­чаев. Страховые компании при заключении договоров иму­щественного страхования стремятся избежать сделок, где есть большой коэффициент кумуляции.

Коэффициент убыточности, «степень убыточности», «степень ущербности»:

           

Данный показатель меньше или равен единице. Превы­сить единицу он не может, так как это означало бы унич­тожение всех застрахованных объектов более чем в один раз.

Средняя страховая сумма на один объект (договор) стра­хования :

.

Объекты имущественного страхования обладают различ­ными страховыми суммами. Поэтому в актуарных расчетах применяются различные методы подсчета средних величин.

Средняя страховая сумма на один пострадавший объект (Спо):

.

Каждый из пострадавших объектов страховой совокуп­ности имеет свою индивидуальную страховую сумму, ко­торая отклоняется от средней величины. Расчет этих сред­них величин имеет большое практическое значение.

Отношение средних страховых сумм называется в практике страхования тяжестью риска:

Тр = .

С помощью этого отношения производятся оценка и переоценка частоты проявления страхового события.

Убыточность страховой суммы, вероятность ущерба:

;          

Иное соотношение (Ус > 1) недопустимо, так как это означало бы недострахование. Убыточность страховой сум­мы можно также рассматривать как меру величины риско­вой премии.

Норма убыточности в процентах:

;          0 < Ну  < 1.

Для практических целей исчисляют нетто-норму убы­точности и брутто-норму убыточности. Величина нормы убыточности свидетельствует о финансовой стабильности данного вида страхования.

Частота ущерба:

;          Чу < 1.

Показатель выражает частоту наступления страхового случая. Частота ущерба всегда меньше единицы. При пока­зателе частоты, равном единице, налицо достоверность на­ступления данного события для всех объектов. Частота ущер­ба обычно выражается в процентах к числу объектов страхования. Страховая статистика требует установления фак­торов, оказавших влияние на частоту ущерба. Влияние отдельных факторов является предпосылкой образования рис­ковых групп.

Тяжесть ущерба (g). Различают полный и частичный ущербы.

Полный ущерб – когда при наступлении страхо­вого случая причиняется ущерб, равный действительной стоимости застрахованного имущества.

Частичный – когда имущество не уничтожено, а только повреждено. Обычно имеется несколько признаков, которые оказывают влияние на тяжесть ущерба: страховая сумма, величина объекта страхования (например, тоннаж судна), величина застрахованного имущества, продолжительность времени ущерба и некоторые другие.

Тяжесть ущерба, которую также называют степенью или размером ущерба, вероятностью распространения ущерба, показывает, какая часть страховой суммы уничтожена. Тяжесть ущерба можно выразить математически как про­изведение коэффициента ущербности (Ку = S Q / S Sm)  и отношения средних страховых сумм (S Sm/m : S.Sn/n) (тяжесть риска Тp):

g = Ку * Тp.

Тяжесть ущерба, связанная с наступлением страхового случая, в любом виде страхования обусловлена качества­ми, присущими объекту страхования. Если частота ущерба показывает объекты страховой совокупности, поврежден­ные в результате проявления риска, то тяжесть ущерба показывает среднюю арифметическую ущерба (среднего обеспечения) по поврежденным объектам страхования по отношению к средней страховой сумме всех объектов:

.

Тяжесть ущерба снижается с увеличением страховой суммы – это необходимо учитывать по каждой рисковой группе.

С помощью страховой статистики изучаются частота ущерба и убыточность страховой суммы по всем видам имущественного страхования, по каждой рисковой группе. Статистическими методами учитываются причины ущерба и их распределение во времени и пространстве.

Анализируя ежегодные статистические данные, страхов­щик имеет возможность выявлять положительные и нега­тивные факторы, оказывающие влияние на работу страхо­вой организации и принимать необходимые меры по обеспечению рентабельности страховых операций.

Страховой рынок подразделяется на отрасли имущественного, личного страхования, страхования ответственности и социального страхования.

Объектами имущественного страхования являются основные и оборотные фонды предприятий, организаций, домашнее имущество граждан.

К основным абсолютным показателям этой отрасли относятся:

страховое поле (N_max),

число застрахованных объектов (заключенных договоров) (N),

число страховых случаев (n_c),

число пострадавших объектов (n_П), страховая сумма застрахованного имущества (S), страховая сумма пострадавших объектов (Sп), сумма поступивших платежей (V, ), сумма выплат страхового возмещения (Q). На основе абсолютных показателей определяются различные относительные и средние показатели: частота страховых случаев, доля пострадавших объектов, опустошительность страховых случаев, полнота уничтожения, коэффициент выплат, убыточность страховой суммы, средние страховые суммы пострадавших и застрахованных объектов, средняя сумма страхового возмещения, средний коэффициент тяжести страховых событий и т.д. Особое внимание уделяется расчеты страховых тарифов: нетто-ставки и брутто-ставки, динамике показателей работы страховых организаций.

Пример 1.

Имеются данные страховых организаций района о добровольном страховании имущества граждан:

Страховое поле (N_max)………………………………………………………………………256250

Число заключенных договоров (число застрахованных объектов) (N)……………… 102500

Сумма застрахованного имущества (S), тыс. руб……………………………………………..198350

Поступило страховых взносов (V, ), тыс. руб……………………………………….2800

Страховые выплаты (Q) тыс. руб…………………………………………………………..1680

Число пострадавших объектов (М)…………………………………………………………2050

Определить показатели, характеризующие деятельность страховых организаций.

Решение.

1.Степень охвата страхового поля:

d = N/ N_max = 102500 / 256250 = 0,4 или 40%.

2. Частота страховых случаев:

Чс = М / N = 2050 /102500 = 0,02 = 2%.

3. Средняя страховая сумма:

 = S / N = 198350 / 102500 = 1,9351 тыс. руб

4. Средняя сумма страхового взноса:

 = V / N = 2800 / 102500 = 27, 317 руб

5. Средняя сумма страховых выплат:

 = Q / n_П = 1680 / 2050 = 819,512 руб.

6. Коэффициент выплат:

К_В = Q / V = 1680 / 2800 = 0,60 = 60%.  Н_у=Q/ (норма убыточности).

7. Убыточность страховой суммы:

q = Q/S = 1680/198350 = 0,0085

8. Коэффициент тяжести страховых событий:

К_Т =  / = 819,512/1935,1 = 0,4235 = 42,35%.

9. Коэффициент финансовой устойчивости (с доверительной вероятностью 0,954, при которой t=2):

К_Ф = t *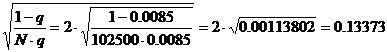

Чем меньше данный коэффициент, тем устойчивее финансовое состояние.

10. Коэффициент финансовой устойчивости страхового фонда

К_Ф.У.= /Q = .2800/1680 = 1,66 = 166%

Пример 2.

Результаты работы страховых организаций в I полугодии характеризуется следующими данными:

Организация	Страховой взнос, V тыс. руб.	Коэффициент выплат, КВ	Выплаты W= КВ/V
1 2 3	400 500 700	0,5 0,6 0,2	200 300 140
Итого	1600	-	640

Определить:

1) средний коэффициент выплат;

2) абсолютную сумму дохода страховых операций;

3) относительную доходность.

Решение.

1. Коэффициент выплат рассчитывается по формуле:

К_В=Q/V.

    Средний коэффициент выплат составит:

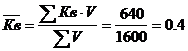= 40 %.

2. Абсолютная сумма дохода определяется разностью взносов и выплат:

 тыс. руб.

3. Относительная доходность (процент доходности) равна:

К_Д= 60%.

Пример 3.

Имеются данные страховых компаний о добровольном страховании имущества, тыс.руб.:

Район	Базисный период			Отчетный период
	Страховая сумма, SО	Страховые выплаты, Q	Коэффициент убыточности, qО	Страховая сумма, S1	Страховые выплаты, Q1	Коэффициент убыточности, q1
1 2	40000 80000	112 128	0,0028 0,0016	56000 84000	140 168	0,0025 0,0020
Итого	120000	240	-	140000	380	-

Определить:

1) индивидуальные индексы убыточности по каждому району;

2) по двум районам индексы средней убыточности:

а) переменного состава,

б) постоянного состава,

в) структурных сдвигов.

Решение.

1. Темп изменения убыточности i_q=q₁/q_0.

По району 1: i_q1 = 0,8929 или 89,3%, т.е. убыточность снижается на 10,7%

По району 2: i_q2 = 1,25 – убыточность возросла на 25%.

2. а) индексы средней убыточности переменного состава равен:

I=,

т.е. средняя убыточность возросла на 10 % за счет влияния двух факторов: изменения коэффициента убыточности и размера страховых сумм.

Этот индекс можно представить иначе, заменив сумму выплат произведением страховой суммы на коэффициент выплат: W=Sq

Тогда индекс средний убыточности переменного состава примет вид:

I=,

б) индекс средней убыточности постоянного состава равен:

I_q== 105,8%

Т.е. средняя убыточность возросла на 5,81% за счет увеличения страховых выплат (убыточности).

в) влияние размера страховых сумм на динамик средней убыточности изучается с помощью индекса структурных сдвигов:

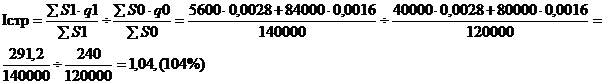
Средняя убыточность дополнительно повысилась на 4% за счет роста страховой суммы в первом районе.

Индекс структурных сдвигов можно определить, используя взаимосвязь индексов:

I_стр  = I/I_q = 1,1 / 1,058 = 1,04