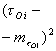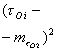Пусть на входе имеется простейший поток заявок с интенсивностью ![]() и загрузкой
и загрузкой ![]() . Среднее значение времени ожидания завершения начатого обслуживания одной заявки равно:
. Среднее значение времени ожидания завершения начатого обслуживания одной заявки равно:
 (7)
(7)
где ![]() - среднее время обслуживания заявок,
- среднее время обслуживания заявок, ![]() ,
,
![]() - параметр потока обслуживания;
- параметр потока обслуживания;
![]() -коэффициент загрузки;
-коэффициент загрузки;
![]() - коэффициент вариации времени обслуживания.
- коэффициент вариации времени обслуживания.
В формуле (7) ![]() и
и ![]() берутся в квадрате, т.е.
берутся в квадрате, т.е. ![]() и
и ![]()
![]() ,
,
где ![]() - среднее квадратическое отклонение времени обслуживания.
- среднее квадратическое отклонение времени обслуживания.
Воспользуется формулой Полячека — Хинчина для определения средней длины очереди ![]() и среднего числа заявок в системе
и среднего числа заявок в системе ![]() :
:
![]() (8)
(8)
![]()
Среднее время ожидания при произвольном законе распределения времени обслуживания можно выразить через время ожидания ![]() при постоянном времени обслуживания и его коэффициент вариации:
при постоянном времени обслуживания и его коэффициент вариации:
![]()
Формулой Полячека—Хинчина можно воспользоваться для определения среднего времени пребывания заявки в очереди ![]() и среднего времени пребывания заявки в системе массового обслуживания
и среднего времени пребывания заявки в системе массового обслуживания ![]() при простейшем потоке заявок с интенсивностью
при простейшем потоке заявок с интенсивностью ![]() и произвольным распределением времени обслуживания с математическим ожиданием
и произвольным распределением времени обслуживания с математическим ожиданием ![]() и коэффициентом вариации
и коэффициентом вариации ![]() :
:
![]()
![]()
Простое выражение для времени ожидания заявок в очереди будет получено при экспоненциальном законе распределения времени обслуживания:
![]()
Распределение количества заявок в системе равно
![]()
Это выражение называется геометрическим законом.
При многомерных простейших потоках с интенсивностью, суммарный поток будет пуассоновским. Его интенсивность
![]() (9)
(9)
При произвольных случайных потоках суммарный поток приближается к простейшему. В практических задачах обычно пользуются суммарным простейшим потоком и получают характеристики с некоторым приближением.
В первую очередь нас интересует продолжительность ожидания заявок в очереди при многомерном потоке. На нее наибольшее влияние оказывают различия во времени обслуживания заявок разных типов, которые характеризуются дисперсией распределения времени обслуживания суммарного потока. Для повышения эффективности обслуживания при бесприоритетной дисциплине желательно так подобрать алгоритмы, чтобы длительности обслуживания разных заявок были более или менее близкими. Рассмотрим практическую задачу.
Пример 17.
Имеется набор программ для решения 20 задач. Интенсивности поступления потоков задач и время работы программ указаны в табл. 9.
Таблица 9
Характеристики потоков заявок и процесса обслуживания
|
Н-р задачи |
|
|
Н-р задачи |
|
|
|
1 |
0,11 |
1,0 |
11 |
0,02 |
2,5 |
|
2 |
0,05 |
1,1 |
12 |
0,03 |
2,6 |
|
3 |
0,09 |
1,2 |
13 |
0,01 |
2,7 |
|
4 |
0,20 |
1,3 |
14 |
0,05 |
2,8 |
|
5 |
0,06 |
1,6 |
15 |
0,02 |
2,9 |
|
6 |
0,02 |
IJ |
16 |
0,03 |
3,1 |
|
7 |
0,01 |
1,8 |
17 |
0,03 |
3,2 |
|
8 |
0,01 |
1,9 |
18 |
0,02 |
3,6 |
|
9 |
0,03 |
2,0 |
19 |
0,03 |
3,8 |
|
10 |
0,02 |
2,1 |
20 |
0,02 |
3,9 |
Определим пропускную способность системы массового обслуживания для решения 20 представленных задач. Оценим, какая очередь появится в этой системе — ограниченная или неограниченная.
Если заданная система не в состоянии обслужить указанный поток заявок, то ее целесообразно разбить на две системы. В первую систему включим 10 задач (программ решения этих задач), во вторую — оставшиеся 10 задач. По полученным системам определим среднюю длину очереди, среднее время ожидания в очереди и среднее время пребывания заявок в системе.
Решение.
1. Определим пропускную способность заданной системы:
![]()
Величина ![]() , следовательно, система не в состоянии обслужить поток в 20 задач. В ней будет образовываться возрастающая неограниченная очередь.
, следовательно, система не в состоянии обслужить поток в 20 задач. В ней будет образовываться возрастающая неограниченная очередь.
Таблица 10
Схема расчета
|
Номер задачи |
|
|
|
Номер задачи |
|
|
|
|||
|
1 |
1,0 |
-0,57 |
0,3249 |
11 |
2,5 |
-0,61 |
0,3721 |
|||
|
2 |
1,1 |
-0,47 |
0,2209 |
12 |
2,6 |
-0,51 |
0,2601 |
|||
|
… |
… |
… |
… |
… |
… |
… |
… |
|||
|
9 |
2,0 |
0,43 |
0,1849 |
19 |
3,8 |
0,69 |
0,4761 |
|||
|
10 |
2,1 |
0,53 |
0,2809 |
20 |
3,9 |
0,79 |
0,6241 |
|||
- Распределим задачи по предложенным в условии двум системам и определим их пропускные способности:
![]()
![]()
Приблизительное равенство пропускных способностей двух систем подтверждает, что с этой точки зрения деление проведено удачно. Кроме того, ![]() следовательно, очереди будут конечной длины.
следовательно, очереди будут конечной длины.
- Интенсивность суммарных входящих потоков новых систем по формуле (9), 1/ч составит:
![]()
- Рассчитаем дисперсии каждой системы. Расчет проведем в табл. 10.
Отсюда
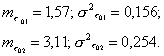
5. Найдем среднюю длину очереди до начала обслуживания каждой системы по формуле (8):
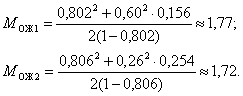
6. Определим среднее время пребывания заявки в системе и среднее время ожидания ее в очереди, ч:
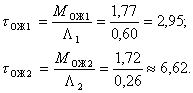
Среднее время пребывания в системах можно определить, используя формулу Полячека — Хинчина:
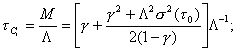
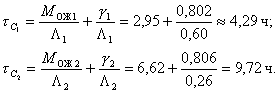
Необходимо заметить, что расчеты по формулам для определения условного среднего времени ожидания в очереди при учете времени переключения достаточно сложны. По этой причине, они проводятся по разработанным алгоритмам и программам на ЭВМ. Оценка эффективности на основе критериев теории массового обслуживания позволяет выработать рекомендации по существенному улучшению работы ЭВМ и их эксплуатации на ВЦ.