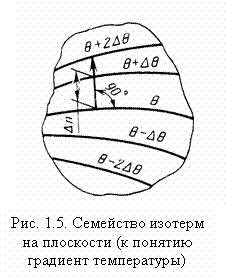
 Рассмотрим элемент изотермической поверхности площадью dF (рис. 1.6). По направлению нормали n покажем вектор grad θ. Он, как уже отмечалось, направлен в сторону повышения температуры. Следовательно, поток теплоты, который представим в виде вектора dQ, направлен в противоположную сторону, поскольку теплота переносится от более нагретых участков тела к менее нагретым.
Рассмотрим элемент изотермической поверхности площадью dF (рис. 1.6). По направлению нормали n покажем вектор grad θ. Он, как уже отмечалось, направлен в сторону повышения температуры. Следовательно, поток теплоты, который представим в виде вектора dQ, направлен в противоположную сторону, поскольку теплота переносится от более нагретых участков тела к менее нагретым.
В 1822 г. Ж.-Б. Фурье высказал гипотезу о том, что количество теплоты dQ, проходящее через элемент поверхности dF за время dτ, пропорционально градиенту температуры, т.е.
dQ=-λ grad θ dF dτ. (1.1)
Знак «минус» в формуле (1.1) показывает, что вектор теплового потока направлен в сторону, обратную направлению вектора grad θ. Гипотеза Фурье была подтверждена в дальнейшем большим количеством экспериментов, причем отмечено, что коэффициент пропорциональности λ является одной из физических характеристик вещества, по которому распространяется теплота. Эту характеристику называют коэффициентом теплопроводности материала.
 Установим размерность коэффициента теплопроводности. Для этого представим выражение (1.1) в скалярной форме и проставим в нем размерности величин: dQ, Дж; grad θ, оС/м; dF, м2; dτ, с. Тогда получим λ в Дж/(м × с × оС) или Вт/(м × оС).
Установим размерность коэффициента теплопроводности. Для этого представим выражение (1.1) в скалярной форме и проставим в нем размерности величин: dQ, Дж; grad θ, оС/м; dF, м2; dτ, с. Тогда получим λ в Дж/(м × с × оС) или Вт/(м × оС).
![]() (1.2)
(1.2)
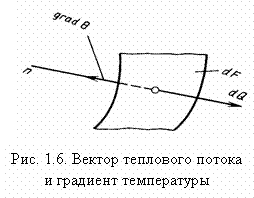
представляющее собой количество теплоты, проходящее в единицу времени через единицу площади изотермической поверхности, принято называть плотностью теплового потока, Вт. Подставляя выражение (1.2) в формулу (1.1) получим
q= - λ grad θ, (1.3)
где q – вектор плотности теплового потока.
Формулой (1.3) представляют обычно основной закон теплопроводности (закон Фурье), гласящий, что плотность теплового потока прямо пропорциональна градиенту температуры.
Если требуется рассчитать количество теплоты, прошедшей через изотермическую поверхность площадью F за время τ, то, интегрируя выражение (1.1), получаем
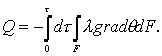 (1.4)
(1.4)
В формуле (1.4) мы не выносим коэффициент теплопроводности за знаки интегралов, потому что λ, не является для данного материала величиной постоянной, а зависит от температуры.