Основываясь на законе Фурье, можно решать задачи, возникающие при описании тепловых процессов в твердых телах различной формы. Распространенной является задача о передаче теплоты через плоскую стенку, на одной поверхности которой действует равномерно распределенный источник теплоты плотностью q, а на другой – сток плотностью  q₁.

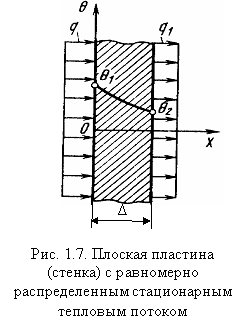Если процесс теплообмена не установился, то q_{1 ≠} q, а температуры поверхностей стенки θ₁ и θ₂ непрерывно меняются. При установившемся теплообмене (рис. 1.7) q_{1 =} q, а θ₁ и θ₂  сохраняют свои значения во времени. Условия задачи, показанной на рис. 1.7, позволяют полагать температурное поле в пластине стационарным одномерным, и поэтому закон Фурье можно представить в виде

.

Предположим далее, что коэффициент теплопроводности зависит от температуры, причем зависимость λ = λ(θ) известна. Введем новую переменную

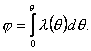
Тогда , что позволяет вместо выражения закона Фурье написать  Разделяя переменные, получаем  Интегрирование последнего выражения  дает

Постоянную С определяем с помощью одного из граничных условий (при x=0 θ=θ₁). Изменив в соответствии с этим условием верхний предел интегрирования, получаем

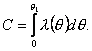
Действуя аналогичным способом, с учетом второго граничного условия (при x=Δ θ=θ₂), запишем выражение φ  в виде

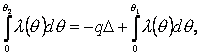
откуда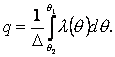       

Эта формула позволяет рассчитать любую из трех величин q, θ₁ или θ₂  по заданным значениям двух других или известному закону  λ(θ). Пусть, например, зависимость коэффициента теплопроводности от температуры описывается линейным законом  Тогда

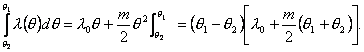
Следовательно, в данном случае

Если при заданном q необходимо рассчитать значение температуры θ₁  или θ₂, то предыдущее выражение можно привести  к виду

и решать квадратное уравнение относительно искомой величины.

Возвращаясь к выражению q, отметим, что в соответствии с известным из математики правилом

где - среднее значение монотонной функции    в интервале   можем написать

Это позволяет сделать важный вывод о том, что, используя закон Фурье, можно вместо переменного значения λ(θ) применить среднее в интервале действующих температур постоянное значение коэффициента теплопроводности λ и этим существенно упростить расчетные формулы без потери точности расчета.

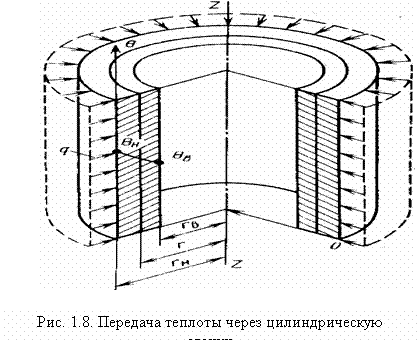
Переходим к рассмотрению вопроса о теплопередаче через цилиндрическую стенку. Пусть на ее наружной поверхности радиусом r_н  (рис. 1.8) действует источник теплоты, создающий равномерно распределенный поток плотностью q. Поскольку процесс теплообмена установился, то температура в любой точке наружной θ_н и внутренней θ_в поверхности во времени не меняется. Изотермические поверхности будут иметь форму цилиндров, коаксиальных оси Z. При установившемся тепловом режиме через любую изотермическую поверхность радиусом r в единицу времени протекает одно и тоже количество теплоты. Следовательно, плотность теплового потока q(r) меняется в зависимости от r, увеличиваясь при переходе от наружной к внутренней поверхности обратно пропорционально текущему значению r. Имея это в виду, а также положив начало координат на поверхности цилиндра в точке 0, закон Фурье представим в виде

Так как   то      и  

Разделяя переменные и интегрируя, получаем

Применяя полученное выражение поочередно к граничным условиям на наружной и внутренней поверхности цилиндра, запишем

  и   

Вычитая из первого выражения второе, получаем

откуда                                                

Сопоставим между собой перепады температур на поверхностях плоской и цилиндрической стенок при условии, что плотность теплового потока q, подведенного к каждой из них, одинакова. Приравнивая выражения q друг к другу, получаем