В технологической теплофизике значительно чаще, чем методы непосредственного интегрирования и интегральных преобразований, применяют метод источников теплоты. Он представляет собой гибкий, удобный в инженерных приложениях математический аппарат, позволяющий описывать тепловые явления в различных технологических системах. С помощью метода источников сравнительно просто можно написать интеграл, удовлетворяющий дифференциальному уравнению теплопроводности и условиям однозначности; дальнейшей задачей является лишь вычисление интеграла. В этом одно из преимуществ метода источников по сравнению с другими аналитическими методами, где отыскание вида интеграла, удовлетворяющего дифференциальному уравнению теплопроводности и условиям однозначности, представляет для более или менее сложных технологических условий значительные трудности.
Основные положения метода источников состоят в следующем:
1 Источник или сток любой формы, движущийся или неподвижный, действующий временно или непрерывно, может быть представлен как система точечных мгновенных источников (стоков) теплоты. Назовем это положение принципом конструирования решений.
2 Процесс распространения теплоты в теле ограниченных размеров может быть представлен как процесс распространения теплоты в неограниченном теле, если фактически действующие источники дополнить некоторой системой фиктивных источников или стоков теплоты. Это положение назовём принцип отражения источников.
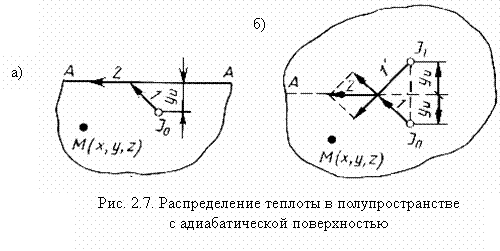
Как следует из изложенного, принцип конструирования решений применяют для описания особенностей источников теплоты, действующих в неограниченном теле, описание же особенностей формы нагреваемых тел и граничных условий на их поверхностях выполняют на основе принципа отражения источников. Покажем применение последнего при описании процесса распространения теплоты в полупространстве с адиабатической поверхностью (граничное условие второго рода qs = 0). Пусть в полупространстве действует источник J (рис. 2.7, а). Тепловой поток, движущийся от источника в каком-либо направлении 1 в сторону граничной поверхности, достигнув последней, в силу условия нетеплопроводности границы должен повернуть и далее двигаться в направлении 2. Если такой же источник действует в неограниченном теле (рис. 2.7, б), то тепловой поток пересечет плоскость АА, находящуюся внутри неограниченного тела, но не являющуюся граничной и адиабатической, и будет продолжать двигаться в направлении 1.
Теперь поместим в неограниченном теле симметрично источнику Jo источник J1. Встречный тепловой поток, идущий в направлении 1, складываясь с тепловым потоком 1, создает равнодействующую, имеющую направление 2, т. е. то же направление, что и в полупространстве с адиабатической граничной поверхностью. Следовательно, процесс распространения теплоты в полупространстве можно представить как часть процесса в неограниченном теле, но с дополнительным источником J1. Поэтому температура ![]() (Jо) в любой точке М (x, y, z) полупространства равна температуре аналогичной точки неограниченного тела
(Jо) в любой точке М (x, y, z) полупространства равна температуре аналогичной точки неограниченного тела ![]() , где
, где ![]() — температуры, возникшие в неограниченном теле от источников Jo и J1 соответственно. Итак, при ГУ2 (qs=0)
— температуры, возникшие в неограниченном теле от источников Jo и J1 соответственно. Итак, при ГУ2 (qs=0)
![]() .
.
.