Для повышения точности измерений рекомендуется производить не одно, а несколько измерений одной и той же величины C при одних и тех же условиях. При многократных измерениях погрешность измерения от случайных ошибок уменьшается в ![]() раз, где n – число измерений.
раз, где n – число измерений.
На основе закона нормального распределения случайных величин можно многократным измерением одних и тех же величин одним и тем же измерительным средством уменьшить влияние случайных ошибок, так как они усредняются, и в итоге повышается точность результата измерения.
Это действие усреднения результатов многократных измерений подтверждается народной пословицей «семь раз отмерь – один раз отрежь». Пословица обращает внимание на то, что однократное «отмеривание» может быть неточным, а семикратное «отмеривание» предохраняет от промахов.
Количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей.
Оценками рассеяния результатов в ряду измерений могут быть:
· размах;
· средняя арифметическая погрешность (по модулю);
· средняя квадратическая погрешность или стандартное отклонение (среднее квадратическое отклонение, экспериментальное среднее квадратическое отклонение);
· доверительные границы погрешности (доверительная граница или доверительная погрешность).
Размах – это оценка Rn рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле
Rn = Хmax – Xmin,
где Хmax и Хmin – наибольшее и наименьшее значения физической величины в данном ряду измерений.
Рассеяние обычно обусловлено проявлением случайных причин при измерении и носит вероятностный характер.
Проведя несколько повторных измерений одной и той же величины и получив различные результаты Xi, определяют среднее арифметическое значение ряда измерений ![]() и принимают его за истинное значение измеряемой величины Cист, т.е. принимают Cист =
и принимают его за истинное значение измеряемой величины Cист, т.е. принимают Cист = ![]() :
:
![]() =
= 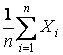 ,
,
где n – число единичных измерений в ряду.
Средняя квадратическая погрешность результатов единичных измерений в ряду измерений – это оценка S рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около их среднего значения, вычисляемая по формуле
S= 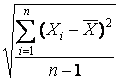 ,
,
где Хi – результат i-го единичного измерения; `Х — среднее арифметическое значение измеряемой величины из n единичных результатов.
На практике широко распространен термин среднее квадратическое отклонение – (СКО). С точки зрения упорядочения совокупности терминов, родовым среди которых является термин «погрешность измерения», целесообразно применять термин «средняя квадратическая погрешность» (СКП). При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений.
Ценность результата многократных измерений значительно повышается, если кроме среднего арифметического значения ![]() будет определена средняя квадратическая погрешность среднего арифметического в виде S`Х, которая зависит от значения S и количества проведения измерений n:
будет определена средняя квадратическая погрешность среднего арифметического в виде S`Х, которая зависит от значения S и количества проведения измерений n:
S`Х = ![]() =
= 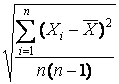 .
.
При ответственных измерениях проводят ряд повторных измерений и на основе полученных результатов всех измерений подсчитывают среднее арифметическое значение ![]() и среднюю квадратическую погрешность S, а потом и погрешность среднего арифметического S`Х.
и среднюю квадратическую погрешность S, а потом и погрешность среднего арифметического S`Х.
Доверительные границы погрешности результата измерений – это наибольшее и наименьшее значения погрешности измерений, ограничивающие интервал, внутри которого с заданной вероятностью находится искомое (истинное) значение погрешности результата измерений.
Доверительные границы распределения вычисляются как ± t S, ± t S`Х, где S, S`Х – средние квадратические погрешности соответственно единичного и среднего арифметического результатов измерений; t – коэффициент, зависящий от доверительной вероятности Р и числа измерений n.
t = 1 при Р = 35 %;
t = 2 при Р = 94,5 %;
t = 3 при Р = 99,73 %.
Для нормального закона распределения случайных величин используется t = 3.
Таким образом, результат измерения или истинное значение измеряемой величины Xист представляется так:
Xист = ![]() ± 3 S`Х или Xист =
± 3 S`Х или Xист = ![]() ±
± ![]() .
.
Полученный результат измерения не является одним конкретным числом, а представляет собой интервал, внутри которого с некоторой вероятностью Р находится истинное значение измеряемой величины.
Пример. Для определения размера отверстия опытной детали измерили его нутромером повышенной точности 10 раз (n = 10). При подсчете получили ![]() = 60,012 мм и S = 0,00115 мм. Истинное значение размера отверстия детали представится так:
= 60,012 мм и S = 0,00115 мм. Истинное значение размера отверстия детали представится так:
Xист = 60,012 ± ![]() = 60,012 ± 0,0011 мм.
= 60,012 ± 0,0011 мм.
Результат расчета показывает, что истинное значение размера отверстия опытной детали определено с точностью ± 1,1 мкм и с вероятностью 0,9973, т.е. только в 0,27 % случаев может оказаться, что погрешность будет не 1,1 мкм.
В случае многократных повторных измерений одной и той же величины одним и тем же методом измерения и при отсутствии систематических погрешностей за предельную погрешность измерения в ряду измерений, обозначаемую Dпр, принимается значение, равное ± 3 S. Так, если бы целью десятикратных измерений являлось определение предельной погрешности данного метода измерения, то эта погрешность для любого отдельного измерения будет равна: Dпр = ± 3 S = ± 3 × 0,0011 = ± 0,003 мм.
Если при многократных измерениях появится погрешность больше 3 S, то такую погрешность считают грубой, и результат измерения с такой погрешностью отбрасывают.
Задания к разделу 8: Ответить на вопросы по своему варианту (номер варианта соответствует последней цифре номера зачетной книжки).
|
Номер варианта |
Вопрос |
|
1 |
1. Что такое погрешность результата измерения? 2. Какие погрешности называются случайными? |
|
2 |
1. Что такое погрешность средства измерения? 2. Что такое промах? Причины возникновения промахов. |
|
3 |
1. Что такое истинное значение физической величины? 2. Как отразится на результате измерений следование русской поговорке: «Семь раз отмерь – один раз отрежь»? |
|
4 |
1. Что такое действительное значение физической величины? 2. Что является оценками рассеяния результатов в ряду измерений? |
|
5 |
1. Что такое результат измерения? 2. Что такое размах и как он определяется? |
|
6 |
1. Какая погрешность называется систематической? 2. Что такое средняя квадратическая погрешность результатов единичных измерений в ряду измерений и как она определяется? |
|
7 |
1. Приведите классификацию систематических погрешностей. 2. Что такое средняя квадратическая погрешность среднего арифметического и как она определяется? |
|
8 |
1. Какая погрешность называется постоянной? 2. Что такое доверительные границы погрешности результата измерения? |
|
9 |
1. Какие погрешности называются прогрессивными? 2. Как вычисляются доверительные границы распределения? |
|
10 |
1. Какие погрешности называются периодическими? 2. Как определяется истинное значение измеряемой величины? |