Алгоритм перебирает допустимые решения задачи, отбрасывая заведомо неоптимальные. Для каждого конкретного класса задач определяется способ перебора допустимых решений (ветвление) и метод исключения из перебора неоптимальных решений (вычисление границ).
Решим задачу (2.22) – (2.24) как задачу линейного программирования, отбросив требование целочисленности. Если в оптимальном решении все переменные целые и xi ≥0 
, то, очевидно, что 
– оптимальное решение задачи целочисленного линейного программирования.
Если некоторая компонента xk нецелая, т.е.
xk = [xk] + {xk},
где [xk] – целая часть xk; {xk} – дробная часть xk, то решаем две задачи линейного программирования:
· одну с дополнительным ограничением
xk = [xk];
· другую с дополнительным ограничением
xk = [xk] + 1.
Если одна из этих двух задач, решаемая как задача линейного программирования, дает нецелочисленное решение с компонентой
xr = [xr] + {xr},
то нужно решить две задачи:
· одну с дополнительными ограничениями
xk = [xk], xr = [xr],
· а другую с дополнительными ограничениями
xk = [xk], xr = [xr] + 1.
Таким образом, если некоторое решение 
не является целочисленным, то оно разветвляется на два дополнительных решения 
и 
. Решения и называются следующими за , а решение – предшествующим и .
Пример
Найти решение задачи:
max x1 + x2
x1 + 3x2 ≤ 10;
4x1+x2 ≤ 12;
x1, x2 ≥0, целые.
Решение
Решим задачу без условия целочисленности симплекс-методом.
Шаг 1. Приведем задачу к каноническому виду:
max x1 + x2
x1 + 3x2 + x3 = 10;
4x1 + x2 + x4 = 12;
x1 ≥ 0, x2 ≥ 0.
Составим симплекс-таблицу:
|
БП |
b |
СП |
|
|
-x1 |
-x2 |
||
|
x3 x4 |
10 12 |
1 4 |
3 1 |
|
f |
0 |
-1 |
-1 |
Выбираем разрешающий элемент и выполняем сиплекс-преобразования:
|
БП |
b |
СП |
БП |
b |
СП |
|||
|
-x4 |
-x2 |
-x4 |
-x3 |
|||||
|
x3 x1 |
7 3 |
-1/4 1/4 |
11/4 1/4 |
=> |
x2 x1 |
28/11 26/11 |
-1/11 3/11 |
4/11 -1/11 |
|
f |
3 |
1/4 |
-3/4 |
54/11 |
2/11 |
3/11 |
||
Полученное оптимальное решение:
= (26/11, 28/11)
является вектором с нецелыми компонентами.
Решаем две задачи линейного программирования: одну с ограничением x1 = 2, вторую с ограничением x2 = 3.
Шаг 2а: Решаем задачу с ограничением x1 = 2, тогда
|
max 2 + x2 |
|
2 + max x2 |
|
2 + 3x2 ≤ 10; |
3x2 ≤ 8; |
|
|
8 + x2 ≤ 12; |
Þ |
x2 ≤ 4; |
|
x2 ≥0; |
x2 ≥0. |
Полученное решение:
x2 = 8/3
Шаг 2б: Решаем задачу с ограничением x1 = 3, тогда
max 3 + x2
3x2 ≤ 7;
x2 ≤ 0;
x2 ≥ 0.
Здесь x2 = 0, f2б = 3.
Решение задачи шага 2а нецелочисленное, поэтому решаем две задачи: одну с ограничением x2 = 2, другую с x3 = 3 (при этом остается x1 = 2):
шаг 3а: x1 = 2, получим: x2 = 2, т.е. решение удовлетворяет ограничениям. Целевая функция f3a = 4;
шаг 3б: x1 = 2, получим x2 = 3, Решение недопустимо, так как не удовлетворяет ограничениям задачи.
Возвращаемся к шагу 1 и начинаем ветвление по нецелой компоненте x2 = 28/11.
Необходимо решить две задачи: одну с ограничением x2 = 2, вторую с x3 = 3.
Шаг 2в: Решаем задачу с ограничением x2 = 2, тогда получим:
max x1 + 2
x1 ≤ 10 – 6;
4x1 ≤ 12 – 2;
x1 ≥0.
Решение: x1 = 5/2.
Шаг 2г: Решаем задачу с ограничением x2 = 3, тогда
max x1 + 3
x1 ≤ 10 – 9;
4x1 ≤ 12 – 3;
x1 ≥0.
Решение: x1 = 1, при этом целевая функция f2д = 4.
Так как на шаге 2в получено нецелое решение, выполним шаг 3в и 3г:
шаг 3в: x1 = 2, сохраняя x2 = 2. Это решение удовлетворяет ограничениям. Целевая функция f3в = 4;
шаг 3г: x1 = 3, при x2 = 2 – решение недопустимо.
Алгоритм закончен, так как все ветви окончились целыми решениями (рис. 2.5).
Сравнивая подчеркнутые элементы схемы (рис. 2.5)находим, что оптимальными являются решения шагов 3а, 2г, 3в, причем на 3а и 3в решения совпадают. На шаге 2б значение целевой функции не максимальное, поэтому (2;2) и (1;3) — это оптимальные решения задачи.
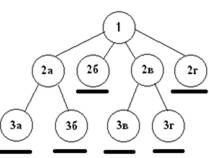
Рис. 2.5. Дерево решения задачи