Требуется перевезти груз из пункта 1 в пункт 14, если известны сеть дорог (рис.4.2) и стоимости перевозки единицы груза между отдельными пунктами сети (поставлены у соответствующих ребер) Необходимо определить маршрут доставки груза из пункта 1 в пункт 14, которому соответствуют наименьшие затраты.

Событиями здесь являются доставки груза в пункты, номера которых записаны в кружках (рис. 4.2), а работами – дороги между отдельными пунктами.

Для того чтобы решить задачу методом динамического программирования, нужно весь процесс доставки груза из пункта 1 в пункт 14 разбить на этапы:

на первом этапе транспорт с грузом из пункта 1 перемещается непосредственно в пункты 2, 3, 4;

· на втором этапе из пунктов 2, 3, 4, – в пункты 5, 6, 7, 8;

· на третьем этапе – из пунктов 5, 6, 7, 8 – в пункты 9, 10, 11;

· на четвертом этапе – из пунктов 9, 10, 11 – в пункты 12, 13;

· на пятом (последнем) этапе из пунктов 12, 13 – в пункт 14.

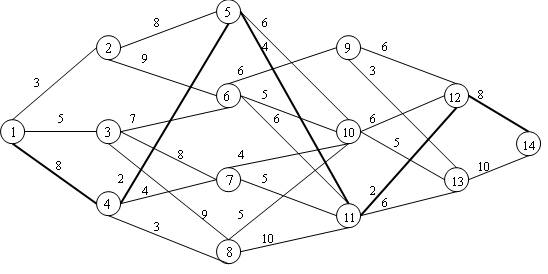
Рис. 4.2. Граф сети дорог

Введем обозначения:

·  – номер этапа, ;

·  – состояние (пункт) на -м этапе;

·  – выбор пути на -м этапе;

·  – стоимость перевозки груза из пункта  в пункт ;

·  – минимальные затраты не перевозку груза из некоторого пункта на -м этапе.

Запишем функциональное уравнение для 5-го этапа:

.

В пункт 14 груз может быть доставлен или из пункта 12, или из пункта 13, поэтому:

;

.

Для 4-го этапа функциональное уравнение имеет вид:

.

Пусть груз на 4-м этапе оказался в пункте 9. Из этого пункта далее можно следовать либо через пункт 12, либо через пункт 13. Тогда

;

,

 при этом минимальные затраты составляют 13.

Если груз оказался в пункте 10, то

;

,

при этом минимальные затраты составляют 14.

Для 11-го пункта получаем

;

,

при этом минимальные затраты составляют 10.

Переходим к 3-му этапу. Для 3-го этапа функциональное уравнение имеет вид:

.

;

,

при этом минимальные затраты составляют 14.

;

,

 при этом минимальные затраты составляют 16.

;

,

при этом минимальные затраты составляют 15.

;

,

при этом минимальные затраты составляют 19.

Рассматриваем 2-й этап.

.

;

,

при этом минимальные затраты составляют 22.

;

;

,

при этом минимальные затраты составляют 21.

;

,

при этом минимальные затраты составляют 16.

Наконец, переходим к 1-му этапу. На 1-м этапе состояние известно – это пункт 1. Поэтому, подставляя это начальное состояние в функцию , сразу получаем значение динамической задачи  и оптимальное управление .

.

;

.

Минимальные затраты при перевозке груза из 1 в пункт 14 составляют 24единицы.