Перед тем, как решать игру, нужно, прежде всего, попытаться ее упростить, избавившись от лишних стратегий. Введем понятие доминирования. Стратегия A_i игрока А называется доминирующей над стратегией A_k, если в строке A_i стоят выигрыши не меньшие, чем в соответствующих клетках строки A_k, и из них, по крайней мере, один действительно больше, чем в соответствующей клетке строки A_k. Если все выигрыши строки A_i равны соответствующим выигрышам строки A_k, то стратегия A_i называется дублирующей стратегию A_k.

Аналогично определяются доминирование и дублирование для стратегий игрока В: доминирующей называется та его стратегия, при которой везде стоят выигрыши не большие, чем в соответствующих клетках другой, и, по крайней мере, один из них действительно меньше; дублирование означает полное повторение одного столбца другим.

Естественно, что если для какой-то стратегии есть доминирующая, то эту стратегию можно отбросить; также отбрасываются и дублирующие стратегии.

Пример 1

Пусть игра задана матрицей табл. 5.6.

Прежде всего, заметим, что в ней стратегия А₅ дублирует стратегию А₂, поэтому любую из них можно отбросить. Отбрасывая A₅, замечаем, что в строке А₁ все выигрыши больше (или равны) соответствующим выигрышам строки А₄, значит А₁ доминирует над А₄. Отбросим А₄ и получим матрицу  (табл. 5.7).

Таблица 5.6 Заданная матрица игры

	В1	В2	В3	В4	В5
А1	4	7	2	3	4
А2	3	5	6	8	9
А3	4	4	2	2	8
А4	3	6	1	2	4
А5	3	5	6	8	9

Таблица 5.7 Удаление дублирующих стратегий

	В1	В2	В3	В4	В5
А1	4	7	2	3	4
А2	3	5	6	8	9
А3	4	4	2	2	8

Замечаем, что некоторые стратегии игрока В доминируют над другими: например, В₃ над В₄ и В₅, a B₁ – над стратегией В₂ (В стремиться отдать поменьше). Отбрасывая столбцы В₂, В₄, В₅, получаем игру  (табл. 5.8).

Таблица 5.8 Удаление не доминирующих стратегий

	В1	В3
А1	4	2
А2	3	6
А3	4	2

Наконец, в табл. 5.8 строка А₃ дублирует A₁, поэтому ее можно отбросить. Окончательно получим игру  (табл. 5.9).

Таблица 5.9 Упрощенная матрица игры

	В1	В3
А1	4	2
А2	3	6

Эту игру уже не упростить. Заметим, что, отбрасывая лишние (дублирующие и заведомо невыгодные) стратегии в игре с седловой точкой, мы придем к решению в чистых стратегиях. Но лучше сразу проверить, не обладает ли игра седловой точкой – это проще, чем сравнивать почленно все строки и все столбцы.

Для простых игр размером или вполне пригоден графический метод, который мы сейчас рассмотрим.

Пусть задана игра  с платежной матрицей (табл. 5.10).

Таблица 5.10 Платежная матрица

	В1	В2	¼	В n
А1	a11	a12	¼	a1n
А2	a21	a22	¼	a2n

Смешанная стратегия первого игрока представляет собой совокупность двух чисел p₁ и p₂, в сумме дающих единицу. Геометрически ее можно представить точкой на единичном отрезке (рис. 5.1), при этом левая крайняя точка отрезка соответствует чистой стратегии A₂ (p₁ = 0, p₂ = 1), а правая – чистой стратегии А₁ (p₁ = 1, p₂ = 0).

Выберем прямоугольную систему координат и отложим на оси абсцисс единичный отрезок для представления смешанных стратегий первого игрока (рис. 5.2). На концах этого отрезка восстановим два перпендикуляра, на которых будем откладывать выигрыши первого игрока, когда он использует чистые стратегии А₂ и А₁.

Пусть второй игрок выбрал стратегию В₁. Тогда при использовании первым игроком чистой стратегии А₂ он получает выигрыш а₂₁ (соответствующая точка на левом перпендикуляре), а при использовании чистой стратегии А₁ – выигрыш а₁₁ (точка на правом перпендикуляре). Соединив эти две точки отрезком прямой, мы получаем график зависимости выигрыша первого игрока М(р,В₁) от смешанной стратегии  при условии, что второй игрок использует чистую стратегию В₁ (рис. 5.2). Точно такие же прямые можно построить для В₁, В₂,…,В_n.

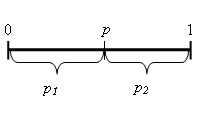
Рис. 5.1. Геометрическое представление смешанной стратегии

Рис. 5.2. График зависимости выигрыша первого игрока от смешанной стратегии

Далее мы должны для каждой смешанной стратегии р, то есть для каждой точки единичного отрезка на оси абсцисс, найти , т.е. нижнюю границу множества n прямых. Эта нижняя граница отмечена (см. рис. 5.2) жирной линией. Та точка отрезка, при которой нижняя граница достигает максимума, соответствует искомой смешанной стратегии , высота максимума дает при этом значение нижней цены игры .

Аналогично можно найти оптимальную смешанную стратегию второго игрока и нижнюю цену игры  в играх  с той лишь разницей, что здесь нужно искать не максимум нижней границы, а минимум верхней границы.

Согласно основной теореме матричных игр решение в смешанных стратегиях существует всегда и .

Для уточнения  и ,  и  нужно найти точку пересечения соответствующих прямых, что в, свою очередь, сводится к решению системы. Рассмотрим это подробно на следующем примере.

Пример 2

Найдем пару оптимальных смешанных стратегий в матричной игре, размером  (табл. 5.11). Графическим методом можно найти стратегии как для первого, так и для второго игрока.

Таблица 5.11 Матрица игры

	В1	В2
А1	1	–1
А2	-2	2

Соответствующие построения приведены на рис. 5.3.

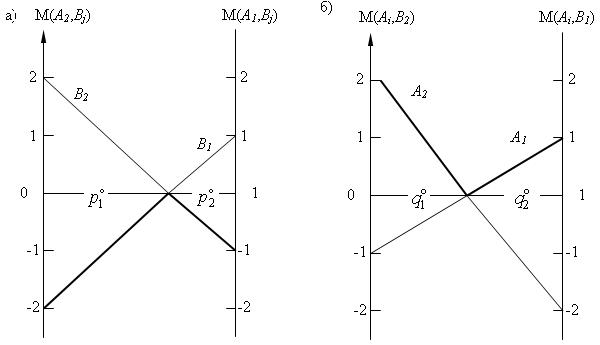
Рис. 5.3. Графический метод поиска стратегий:

а – для первого игрока, б – для второго игрока

Для уточнения  и ,  и , а также v решаем системы уравнений:

                       

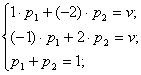
Чтобы составить системы, нужно найти  и , приравнять их к v с учетом того, что компоненты  и  в сумме дают единицу. Из решения систем получим, что:

;            ;       v = 0.