Изучая основные положения теории игр, мы до сих пор рассматривали лишь одну форму представления игры – нормальную. Следует признать, что такая игра выглядит довольно скучно: игроки одновременно выбирают стратегии, получают выигрыши и на этом партия кончается. Временнóй, динамический аспект совершенно не учитывается, в то время как многие реальные игры (те же шахматы) имеют ярко выраженный многоходовой характер и пока не ясно, как их можно привести к нормальной форме.
Познакомимся с другой формой представления игры – позиционной или, как иногда говорят, развернутой. Она наиболее естественна для многоходовых игр, когда игроки делают ходы поочередно.
Игра в позиционной форме представляется деревом игры – графом, вершины которого соответствуют состояниям игры (позициям), а ребра, выходящие из вершин, отображают варианты выбора решений в этих позициях.
Дерево игры строится по следующим правилам:
1) задается начальная вершина – исходная позиция игры;
2) около каждой вершины ставится номер игрока, делающего ход в данной позиции. В тех случаях, когда правилами игры предусмотрены некоторые случайные действия (например, раздача карт), они приписываются случаю – дополнительному фиктивному игроку, имеющему номер 0;
3) из вершин проводятся ребра, соответствующие возможным вариантам ходов в данной позиции. Ребра оканчиваются вершинами, обозначающими новые позиции;
4) если в некоторой позиции ход делается случаем, то на исходящих ребрах записывается соответствующее распределение вероятностей;
5) определяется совокупность конечных вершин, в которых правилами предусматривается окончание игры. У каждой конечной вершины записывается вектор (
), определяющий полезность данного исхода для каждого из игроков (если игроков всего два, то у конечных вершин будет две полезности). Все остальные вершины (позиции) разбиты на (
) множество 
, где 
– множество позиций, в которых выбор альтернативы осуществляется случайным способом с заданным законом распределения (вектором вероятностей), а 
– множество позиций, где ход делает i-й игрок, 
(n – число игроков);
6) для каждого из игроков определяется совокупность информационных множеств (понятие информационного множества мы рассмотрим далее).
Если при выполнении очередного хода игрок не знает всей предыстории игры, т.е. всех выборов на предыдущих ходах (включая и случайные), то он фактически не знает в какой позиции осуществляется его выбор на данном ходе. Такие игры называются играми с неполной информацией. Для описания неопределенности, с которой сталкивается i-й игрок на своем ходе, используется разбиение множества на подмножества, называемые информационными множествами, и принимается, что позиции, принадлежащие одному информационному множеству, для него неразличимы.
Таким образом, делая очередной ход, игрок знает, что он находится в одной из позиций данного информационного множества. При этом он может сделать разумный выбор лишь в том случае, когда число возможных альтернатив в каждой из позиций одно и то же и между ними есть однозначное соответствие. Если каждое информационное множество игры содержит только одну позицию, то получаем игру с
полной информацией, в которой каждый игрок на любом шаге знает всю предысторию процесса игры.
На рис 5.4 приведен пример дерева игры, в которой имеются два игрока, каждый из них делает по одному ходу, выбирая одну из двух альтернатив, причем игрок I делает свой ход в начальной позиции А, а игрок II – в позиции В или С, входящих в одно информационное множество, т.е. он не знает выбора игрока I на первом ходе. В результате выборов игроков может получиться одна из четырех конечных позиций, в которых задана пара выигрышей игроков.
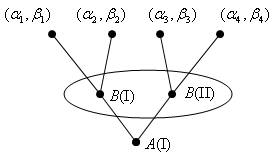
Рис. 5.4. Пример дерева игры
С помощью дерева удобно описывать игры, в которых каждый игрок имеет конечное число ходов и на каждом ходу осуществляет выбор из конечного числа альтернатив, т.е. конечные игры. Для конечных игр справедливо следующее замечательное утверждение: любая конечная игра с полной информацией имеет ситуацию равновесия, определение которой аналогично определению седловой точки (см. раздел 5.2).
Классическим примером игры с полной информацией являются шахматы. Так как эта игра антагонистическая (хотя при обычном турнирном подсчете очков является игрой с ненулевой суммой), то из предыдущего утверждения следует, что она имеет седловую точку, т.е. либо белые побеждают независимо от действий черных, либо черные побеждают независимо от действий белых, либо обе стороны могут обеспечить себе ничью независимо от действий соперника. Однако такая кажущаяся простата является сугубо теоретической, практически в шахматах такое число стратегий, что нахождение оптимальной стратегии и ответ на вопрос, какая из трех возможных альтернатив действительно имеет место, пока не представляются реальными.
Если игра не является конечной, т.е. игроки либо имеют бесконечное число ходов, либо бесконечное число альтернатив на каждом (или некоторых) ходу, то представление игры в виде дерева теряет свою наглядность и становится практически бесполезным. Для таких игр существуют различные виды описания, соответствующие различным классам игр. Наиболее интересным и важным является класс динамических игр. Раздел теории и игр, посвященный динамическим играм, тесно связан с динамическим программированием.
Динамические игры в зависимости от вида выбора (стратегии) подразделяются на многошаговые и дифференциальные. Многошаговые динамические игры, в которых ходы осуществляются в дискретные моменты времени (и, значит, на конечном интервале времени их число конечно), описываются с помощью многошаговых уравнений. Для игр двух лиц такие уравнения имеют вид:
, 
, (5.12)
где 
– фазовые переменные, описывающие состояние процесса игры на k-м шаге (х0 – фиксировано); uk – стратегия (управление) игрока I на k-м шаге; vk стратегия
(управление) игрока II на k-м шаге; N- число ходов. На эти параметры могут быть наложены ограничения, простейшие из которых имеют вид 
(
не ограниченны)
Если игра антагонистическая, то должна быть задана одна функция выигрыша, которую игрок I старается максимизировать, а игрок II – минимизировать (для неантагонистической игры их две). Эту функцию можно задать в виде:
(5.13)
где
Так как из уравнений (5.12) траектория процесса игры однозначно определяется полными векторами стратегий 
то можно записать 
и функцию выигрыша представить в виде:
где
Теперь игру можно представить формально в нормальной форме:
,
в частности, ставить вопрос о существовании седловой точки 
.
Однако представление функции выигрыша в явном виде 
практически возможно лишь в простейших случаях, поэтому нормальная форма здесь мало что дает, а имеет смысл использовать специфику описания динамического процесса в виде (5.12), как это делается в динамичном программировании.
Пусть игра дошла до позиции 
и игрок I решает, как ему выбрать управление 
на (N – 1)-м шаге. В силу аддитивности функции выигрыша (5.13) это управление влияет только на члены 
и 
(на последний в силу уравнения (5.12)).
Гарантированный выигрыш на последнем (N – 1)-м шаге равен:
.
Значит, в позиции игрок I себе обеспечить в лучшем случае выигрыш:
Аналогично, игрок II может себе обеспечить в лучшем случае в позиции проигрыш:
.
Если операции max и min здесь представимы, т.е. выражение в квадратных скобках представляет собой при фиксированном 
функцию от 
, имеющую седловую точку на 
, то
.
Далее будем считать, что на каждого шаге это справедливо, тогда существует седловая точка 
во всей игре.
На (N – 2)-м шаге в позиции 
игрок I с учетом последнего (N-1)-го шага может себе гарантировать выигрыш:
,
а игрок II – проигрыш не более 
.
Рассуждая аналогичным образом, получим последовательность функций 
, которые определяются рекуррентными соотношениями:
(5.14)
Функции аналогичны функциям Беллмана в динамическом программировании. С их помощью определяется решение игры, а именно, цена игры равна 
, а оптимальные стратегии 
получаются последовательной подстановкой в решения задач (5.14) (седловые точки) 
значений фазовых переменных от 
до 
Если выбор стратегий (управлений) в игре осуществляется непрерывно, т.е. стратегии представляют собой функции времени 
, то такие игры описываются, обычно, с помощью дифференциальных уравнений
и интегральных функций выигрыша
.
и носят название дифференциальных игр. Для таких игр также можно построить функцию Беллмана, с помощью которой получается решение игры. Техника тут намного сложнее и эти вопросы рассматривать не будем.