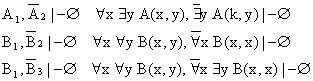Пусть А1, …, Аm, В – формулы. Рассмотрим доказательство секвенции А1, …, Аm ® В.
Доказательство основано на достоверности выражения 
, которая вытекает из теоремы о полноте. Однако достоверность Е не означает выполнимость ØЕ, то есть достоверность пропорциональна невыполнимости. Это следует из определений достоверности и выполнимости, а также из выражения
Чтобы показать, что формулы |- A ® B и |- B ® A достоверны, необходимо доказать невыполнимость формулы 
.
Определение 1: Атом или отрицание атома – литерал f (x); 
.
Определение 2: Формула, в которой символом Ú объединены более одного литерала, называется предложением.
Определение 3: Если с1, …, сk – предложения, а x1, …, xm — различные переменные, содержащиеся в сi (1 £ i £ k), то формула вида 
называется клаузальной формой (сколемовской конъюнктивной формой). 
. Все А можно преобразовать в 
(КФ).
Если А — выполнимо, то и – выполнимо; для невыполнимого А доказать невыполнимость .
Порядок преобразования в клаузальную форму
1) Ограничение свободных переменных
Пусть x1, …, xh – свободные переменные Ì А и преобразовывающие А к виду 
.
2) Переименование переменных
Изменить связанные переменные при к " символе $ или " в формуле так, чтобы было соответствие различных переменных.
3) Удаление символа É
Часть формулы В É С заменим на ØВ Ú С.
4) Перемещение Ø внутри Ú, Ù, ", $:
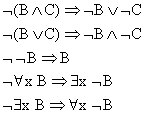
5) Удаление $
Крайний слева член в формуле вида $y B(y) заменяется на B (f (x1, …, xn) ). x1, …, xn – свободные переменные, ограниченные " xi (1 £ i £ k);
f – вновь выбранный функциональный n – местный символ.
При n = 0 он заменяется на вновь выбранную константу, которая до сих пор не применялась. Все это – сколемовская функция и сколемовская постоянная.
Пример:
f-g – сколемовские функции
a – сколемовская постоянная, f — функция
6) Перемещение " вперед
Часть "х перемещается в префиксную часть программы.
7) Перемещение Ú относительно Ù
8) Минимизация
Осуществляется минимизация с сохранением свойства выполнимости. Например, удаляются неоднократно появляющиеся литералы, взаимно отрицающие литералы.
Унификация и правила вывода
Метод резолюций
В рамках этого метода формулируется конструктивный пример n резолюций, который дает алгоритм установления истинности клауз без использования каких-либо аксиом.
.
Пусть дана следующая клауза: 
. Выписываем все по-сылки:
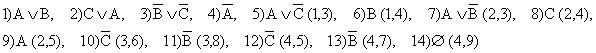
При прямом последовательном склеивании дизъюнктов получили пустое множество, что свидетельствует об истинности исходной клаузы. Приблизительно такой алгоритм реализован при машинном доказательстве теорем. Однако для этой задачи существует более рациональный путь отыскания пустого множества:
.
До сих пор мы рассматривали конъюнктивные противоречия. Исходя из принципа двойственности, метод резолюций можно сформировать относительно дизъюнктивной тавтологии; при этом резолюция изменится на:
Докажем:
Пусть дана клауза: A, A ® B, B ® (A ® C) |—
Запишем исходную клаузу в форме противоречия:
Теперь сделаем это в форме тавтологии:
.
На основе этой таблицы можно установить следующие справедливые отно-шения:
Примеры доказательств тождеств и клауз в логике предикатов
Пример 1
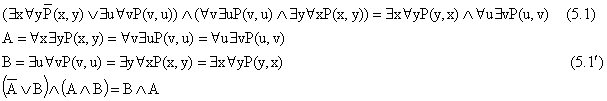
Произведя элементарные преобразования (5.
), мы можем убедиться в справедливости исходного выражения (5.1).
Пример 2
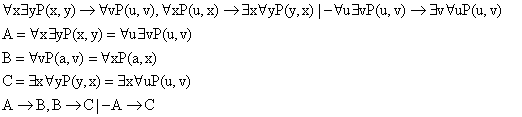
Доказательство справедливости предикатных выражений свелось к процедуре идентификации их с соответствующими выражениями, существующими в логике множеств и в логике высказываний.
Пример 3
Введём обозначения: 
Используя метод резолюций, (5.2¢) представим в виде
(5.2¢¢)
По методу резолюций выражение (5.2¢¢) будет верным, если окажутся верными два противоречия: 
и 
.
Список из восемнадцати клауз (приводился выше) предоставляет две истинные клаузы (6 и 7). Если их представить в форме противоречий, то их можно использовать для нашего случая.
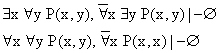
При доказательстве встречаются ошибки в обозначениях, которые сводятся к неправильным выборам типа: вместо может быть 
— неверно.
Пример 4
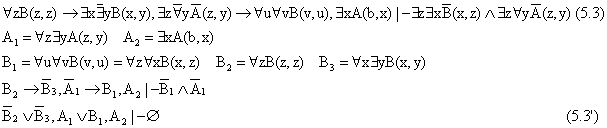
Все склейки клаузы (5.3¢) осуществлены, так как они удовлетворяют таблице из 18 клауз:
