Недетерминированное управление наиболее характерно для систем искусственного интеллекта. Такое управление необходимо потому, что знания накапливаются фрагментарно, и нельзя априори определить цепочку логических выводов, в которых они используются. Другими словами, необходимо методом проб и ошибок выбрать некую цепочку выводов и в случае неуспеха организовать перебор с возвратами для поиска другой цепочки и т. д. Такое управление является предпосылкой проявления гибкости и интеллектуальных способностей, позволяющих найти выход в самых различных ситуациях.
Поскольку эффективность простого поиска низка, возникает необходимость определения пути, по которому следует начать поиск в первую очередь. При эвристическом поиске, например алгоритме А*, разработанном на первых этапах исследования искусственного интеллекта, руководствуются оценочными функциями, которые не всегда бывают точными (имеют априорные значения). Об алгоритме А* рассказано ниже.
В эпоху инженерии знаний возникла идея реализации выводов (поиска) на основе знаний. Шире стали применять эвристические знания (в смысле не обязательно достоверных знаний, т. е. знаний, содержащих нечеткости). В качестве наиболее характерного примера можно привести программу AM, которая открывает новые математические понятия. Как подчеркнул создатель этой программы Д.Б. Ленат, эвристические знании в ней играют важную роль. Эта программа также будет рассмотрена ниже.
Алгоритм А*
Большинство поисковых задач можно сформулировать как задачи поиска в пространстве состояний пути от исходного состояния заданной задачи до целевого состояния путем повторения возможных преобразований (с помощью операторов). При этом для организации поиска в пространстве состояний удобно использовать дерево поиска (или его более общую форму — граф). К основным методам систематического просмотра пространства состояний относятся вертикальный и горизонтальный поиск. В алгоритме А* использованы априорные оценки стоимости пути до целевого состояния (разновидность эвристических знаний), что обеспечивает высокую эффективность поиска.
Описание этого алгоритма удобно рассмотреть на примере игры в восемь, которую использовал Нильсон. Эта игра — минивариант игры в пятнадцать; на поле 3×3 размещены восемь пронумерованных шашек, цель игры — от заданного начального состояния перейти к целевому состоянию так, как показано ниже.
|
2 |
4 |
3 |
|
1 |
2 |
3 |
|
1 |
8 |
5 |
4 |
5 |
6 |
|
|
7 |
6 |
7 |
8 |
|||
|
Начальное состояние Целевое состояние |
||||||
На поле один пустой квадрат: состояние можно изменить, передвигая шашку сверху, снизу, справа или слева на пустой квадрат. Следовательно, в этой игре есть четыре оператора преобразования состояния, соответствующие одному из передвижений шашки на пустой квадрат. А раз так, то не нужно следить за перемещениями какой-либо конкретной шашки, поэтому изменим точку зрения, и будем перемещать пустой квадрат. Теперь просто определить следующие четыре оператора:
1) перемещение пустого квадрата влево (при этом слева есть квадрат);
2) перемещение пустого квадрата вверх (при этом вверху есть квадрат);
3) перемещение пустого квадрата вправо (при этом справа есть квадрат);
4) перемещение пустого квадрата вниз (при этом внизу есть квадрат).
Используя эти операторы, будем осуществлять поиск в пространстве состояний. Рассмотрим также следующую оценочную функцию как функцию, регламентирующую выбор эффективного направления поиска. Пусть f(n) — стоимость оптимального пути к цели от первой вершины (начального состояния) через n вершин дерева поиска. Разделим f(n) и представим ее следующим образом:
f(n)=g(n)+h(n),
где g(n) - стоимость оптимального пути от первой вершины до n-й вершины;
h (n) - стоимость оптимального пути от n-й вершины до цели.
Будем считать, что перемещение одной шашки в игре в восемь имеет стоимость 1, а до цели ведет оптимальный путь с минимальной стоимостью.
В процессе поиска в общем случае нельзя точно знать f(n), поэтому рассмотрим априорное значение ![]() . В момент прохождения n-й вершины g(n) известно, поэтому можно записать
. В момент прохождения n-й вершины g(n) известно, поэтому можно записать
![]()
где ![]() - априорное значение h(n). Если представить пространство поиска в игре в восемь в виде дерева, то g(n) - это глубина от первой вершины до n-й вершины. В качестве h(n), например, выберем число шашек, находящихся не на своих местах. Определив таким образом оценочную функцию, выберем стратегию прохождения вершин (применения операторов), в которых значения функции минимальны.
- априорное значение h(n). Если представить пространство поиска в игре в восемь в виде дерева, то g(n) - это глубина от первой вершины до n-й вершины. В качестве h(n), например, выберем число шашек, находящихся не на своих местах. Определив таким образом оценочную функцию, выберем стратегию прохождения вершин (применения операторов), в которых значения функции минимальны.
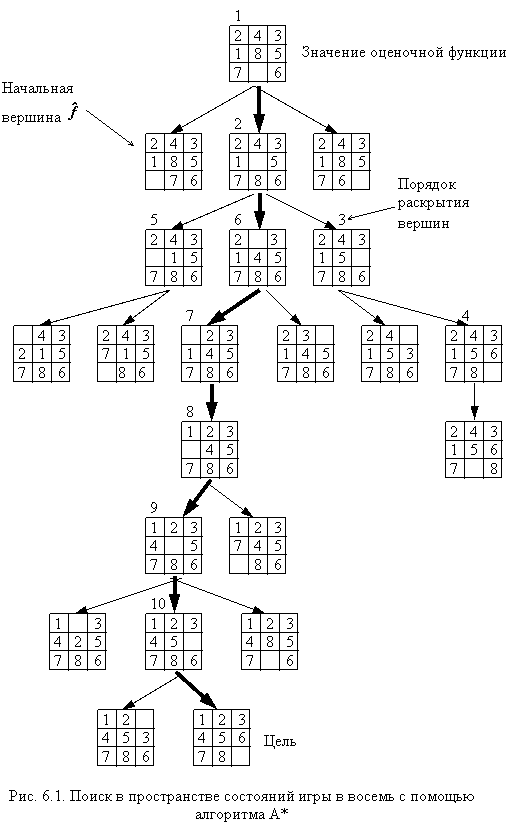
На рис. 6.1 показан результат поиска. Выбираем вершину с наименьшим из значений оценочной функции, указанных цифрами в кружочках, применяем оператор и раскрываем вершину, затем создаем дочерние вершины (при этом не возвращаемся к уже появившимся вершинам). Повторяем эту процедуру до целевого состояния. Цифры слева вверху каждой вершины на рис. 6.1 указывают порядок раскрытия вершин.
Здесь важно, что ![]() , а именно если априорное значение стоимости от n-й вершины до цели (
, а именно если априорное значение стоимости от n-й вершины до цели (![]() ) меньше или равно истинной стоимости оптимального пути к цели (
) меньше или равно истинной стоимости оптимального пути к цели (![]() ), то это гарантирует, что обязательно будет найден оптимальный путь. Поиск с использованием функции (
), то это гарантирует, что обязательно будет найден оптимальный путь. Поиск с использованием функции (![]() ) называется алгоритмом А*.
) называется алгоритмом А*.
В этой игре в качестве ![]() ) выбрано число шашек, находящихся не на своих местах, причем
) выбрано число шашек, находящихся не на своих местах, причем ![]() (не достигнем цели, пока число перемещений меньше числа шашек, находящихся не на своих местах). Следовательно, рис. 6.1 также представляет поиск по алгоритму А*. Если же выбрать
(не достигнем цели, пока число перемещений меньше числа шашек, находящихся не на своих местах). Следовательно, рис. 6.1 также представляет поиск по алгоритму А*. Если же выбрать ![]() , то мы имеем горизонтальный поиск, при котором прежде всего раскрываются близлежащие вершины (число таких вершин возрастает), оптимальный путь при этом в конце концов находится. Если
, то мы имеем горизонтальный поиск, при котором прежде всего раскрываются близлежащие вершины (число таких вершин возрастает), оптимальный путь при этом в конце концов находится. Если ![]() ,то можно доказать, что число вершин, раскрытых при поиске с использованием функции
,то можно доказать, что число вершин, раскрытых при поиске с использованием функции ![]() , всегда меньше, чем при поиске с использованием функции
, всегда меньше, чем при поиске с использованием функции ![]() . А именно, h(n) можно рассматривать как объем эвристических знаний, предсказывающих стоимость пути до цели, следовательно, объем эвристических знаний h2(n) больше, чем h1(n).
. А именно, h(n) можно рассматривать как объем эвристических знаний, предсказывающих стоимость пути до цели, следовательно, объем эвристических знаний h2(n) больше, чем h1(n).
Программа AM
Программа AM, разработанная Д. Б. Ленатом, предназначена для «открытия» новых понятий в области целых чисел. Для руководства «открытиями» (что можно рас
сматривать как своего рода автоматическое обучение) используются эвристические знания самого высокого уровня.
Эта программа, основываясь на 115 заранее заданных фундаментальных понятиях теории множеств и используя 243 эвристических знания, начинает расследование с целью обнаружения новых, еще неизвестных, но интересных понятий. Созданные понятия представляются в виде фрейма с несколькими слотами.
На рис. 6.2 показана структура фрейма ПРОСТЫЕ ЧИСЛА, открытого этой программой. Эвристические знания описываются в форме правил (типа ЕСЛИ—ТО) и добавляются в соответствующие слоты фреймов. Глобальная структура управления основана на механизме «списка заявок»; задания, которые предстоит выполнить, прежде всего, регистрируются в списке заявок с указанием приоритета («интереса»), из списка выбирается задание с наиболее высоким интересом и выполняется. Во время выполнения задания подбираются соответствующие правила (подбираются также правила из фреймов высшего уровня через указатели в слоте ОБОБЩЕНИЕ текущего фрейма, затем эти правила используются.

Устанавливаются слоты ОПРЕДЕЛЕНИЯ, ПРИМЕРЫ, ОБОБЩЕНИЯ, СПЕЦИАЛИЗАЦИЯ, ПРЕДПОЛОЖЕНИЯ, АНАЛОГИ, ИНТЕРЕС, ЦЕННОСТЬ
(вводится оценка — число от 0 до 1000)
Рис. 6.2. Фрейм понятия «простые числа», полученный программой AM
Функции правил можно классифицировать следующим образом:
1) Вставка содержимого в слот специального понятия выполняется при перечислении ПРИМЕРОВ некоторого понятия, при построении ПРЕДПОЛОЖЕНИЙ, при обновлении слота ЦЕННОСТЬ.
Кроме правильных примеров в слоте ПРИМЕРЫ можно привести подтверждающие граничные примеры (в слоте ГРАНИЦЫ), контрпримеры (в слоте НЕУДАЧА), граничные контрпримеры (в слоте ГРАНИЦЫ-НЕУДАЧИ). В слоте ПРЕДПОЛОЖЕНИЯ определяются эквивалентность с другим понятием, особенности, обобщения, связь через некоторый предикат и т. п.
2) Проверка слотов некоторого понятия — проверяя правильность содержимого слота, обнаруживаются интересные факты через систематизацию и связь с другими понятиями (обобщение, особенности и т. д.).
3) Генерация новых понятий — с этой целью используются обобщения, выделение особенностей, обработка контрпримеров, подобие, связь с обратным явлением, синтез функций, проекция, упрощение, прямое произведение множеств и другие операции. Новый фрейм создается и вводится в слот ОПРЕДЕЛЕНИЯ (как описание на языке ЛИСП этого определения);
4) Регистрация нового задания в списке заявок.
5) Критерии оценки интереса к понятию и заданию — используются симметрия, частота появления понятия, индивидуальность, связь с другими интересными понятиями, непрерывность по отношению к последнему заданию (механизм концентрации внимания) и другие факторы.
Процесс поиска в общих чертах сводится к повторению следующих действий: выбору одного из понятий, построению примеров, проверки степени интереса и порождения нового задания (включая генерацию нового понятия). Обращая внимание на степень интереса к понятию, организуется поиск возможности применения различных функций, крайних случаев, обобщений, особенностей и т. п.
Программа AM запускалась несколько раз, всего сгенерировано (открыто) около 200 новых понятий. Примерно половина из них представляют определенный интерес и хорошо известны в математике. К ним относятся следующие понятия:
1) простые числа (2, 3, 5, 7, 11, 13, 17, 19, …: имеют только два делителя) — определяются так, как на рис. 6.2;
2) квадраты простых чисел (4, 9, 25, 49, 121, 169, 289 …: имеют три делителя);
3) однозначность разбиения на простые множители (все числа однозначно представляются в виде произведения простых чисел);
4) все числа (больше 1) можно представить в виде суммы простых чисел;
5) четные числа больше 2 можно представить в виде суммы двух простых чисел (гипотеза Гольдбаха);
6) существование пар простых чисел Р и Р + 2 и другие понятия.
Разумеется, самой программе AM трудно давать названия новым понятиям, такие названия, как простые числа, даются уже позже людьми, интерпретирующими их смысл.
Существенное отличие программы AM от поиска при решении традиционных задач заключается в отсутствии строгих правил поиска. Цель поиска этой программы — максимально проявить самостоятельность (выполнять задания с наивысшим уровнем приоритета). Поиск в бесконечном пространстве организуется за счет того, что из эвристических правил отыскиваются наиболее интересные. (Ленат выдвинул интересную гипотезу: может быть можно провести аналогию между тем, как программа AM делает осмысленные шаги, абстрагируясь от цели, и скрытой в генах информацией, которая руководит направлениями эволюции животного мира?)
Программа AM имеет одно ограничение: ее эвристические правила фиксированы. Чем дольше работает программа, тем меньше эффективность начальных эвристических правил, особенно для новых ситуаций. Преодолеть это ограничение может программа
EURISKO, она обладает механизмом генерации новых эвристических правил под руководством эвристических метаправил.