Направленный отрезок с началом в точке А и концом в точке В называется геометрическим вектором или просто вектором. Обозначается 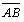 или строчными буквами латинского алфавита со стрелкой сверху:
или строчными буквами латинского алфавита со стрелкой сверху: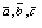 , …Длина отрезка АВ называется длиной или модулем вектора и обозначается:
, …Длина отрезка АВ называется длиной или модулем вектора и обозначается: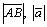 .Если точки А и В совпадают, то вектор называется нулевым . Нулевой вектор обозначается либо
.Если точки А и В совпадают, то вектор называется нулевым . Нулевой вектор обозначается либо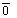 , либо 0 . Нулевой вектор не имеет направления и длина его равна нулю.Два вектора называются коллинеарными , если они лежат на одной прямой или параллельны одной прямой (лежат на параллельных прямых).Два вектора называется равными , если они коллинеарны, имеют одинаковое направление и длину. Произведением
, либо 0 . Нулевой вектор не имеет направления и длина его равна нулю.Два вектора называются коллинеарными , если они лежат на одной прямой или параллельны одной прямой (лежат на параллельных прямых).Два вектора называется равными , если они коллинеарны, имеют одинаковое направление и длину. Произведением 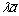 вектора
вектора 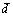 на действительное число
на действительное число 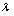 называется новый вектор
называется новый вектор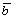 , который обладает свойствами:1о
, который обладает свойствами:1о 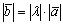 ;2° направление вектора
;2° направление вектора 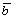 совпадает с направлением вектора
совпадает с направлением вектора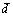 , если
, если 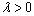 (рис. 2.1, а) и противоположно направлению вектора
(рис. 2.1, а) и противоположно направлению вектора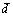 , если
, если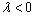 (рис. 2.1, б).
(рис. 2.1, б).

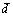 , то говорят что вектор
, то говорят что вектор 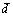 отложен от точки А . Отложим от точки А вектор
отложен от точки А . Отложим от точки А вектор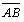 , равный
, равный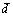 . Затем от точки В отложим вектор
. Затем от точки В отложим вектор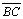 , равный
, равный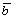 . Вектор
. Вектор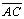 , равный
, равный 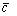 , называется суммой векторов
, называется суммой векторов 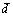 и
и 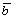 и обозначается:
и обозначается:
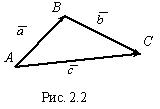 Для любых трех точек А , В , С (рис. 2.2) справедливо равенство (правило треугольника):
Для любых трех точек А , В , С (рис. 2.2) справедливо равенство (правило треугольника):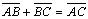 .Умножение вектора на число и сложение векторов называются линейными операциями над векторами.Два вектора называются противоположными , если их длины равны, и они противоположно направлены. Из определения произведения вектора на число следует, что
.Умножение вектора на число и сложение векторов называются линейными операциями над векторами.Два вектора называются противоположными , если их длины равны, и они противоположно направлены. Из определения произведения вектора на число следует, что 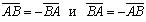 . Разностью векторов
. Разностью векторов  называется вектор
называется вектор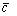 , сумма которого с вектором
, сумма которого с вектором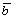 равна вектору
равна вектору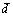 . Обозначается:
. Обозначается: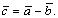 Разность векторов можно определить также равенством:
Разность векторов можно определить также равенством: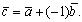 Множество всех векторов на плоскости (в пространстве) образуют линейное пространство.
Множество всех векторов на плоскости (в пространстве) образуют линейное пространство.