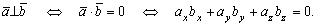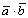Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначение: или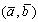.Таким образом, по определению

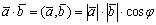
, (2.7)

где угол между векторами. По формуле (2.1)

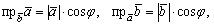
т.е.

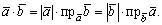
(2.8)

Свойства скалярного произведения векторов (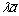ненулевые векторы)

1о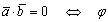.прямой угол (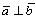),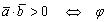острый угол,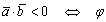тупой угол;2о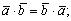.3о. 4o.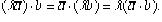

Доказательство Свойства 1о, 2о Справедливость этих свойств вытекает непосредственно из определения. Свойство 3°

.

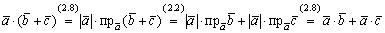
Свойство 4°

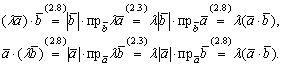
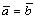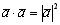Если, то по определению Произведение называется скалярным квадратом вектора 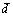Получим формулу для вычисления скалярного произведения через координаты сомножителей. Пусть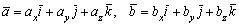, тогда, используя доказанные свойства l° — 4°, получаем:

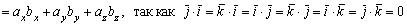(свойство 1о),

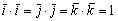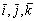(единичные векторы).

Таким образом, скалярное произведение векторов равно сумме попарных произведений соответствующих координат этих векторов:

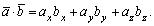
(2.9)

Основные приложения скалярного произведения

1)Вычисление угла между векторами

Из определения скалярного произведения и формул (2.5), (2.9) следует, что

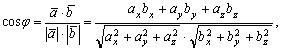
(2.10)

где угол между векторами.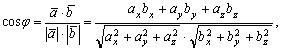

2)Вычисление проекции одного вектора на другой

Из равенств (2.8) находим:

.

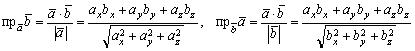
3)Условие перпендикулярности векторов

Используя свойство 1о и формулу (2.9) , получаем: