Математическое моделирование экономических явлений и процессов является важным инструментом экономического анализа: дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его

внутреннюю структуру и внешние связи. Модель – условный образ объекта исследования (управления), отражающий его свойства. Модель конструируется субъектом управления с тем, чтобы отобразить характерные свойства, структурные и функциональные параметры объекта, его взаимосвязи, существенные для достижения цели управления. Содержание метода моделирования составляет:

· конструирование модели на основе предварительного изучения объекта;

· выделения его существенных характеристик;

· экспериментальный или теоретический анализ модели;

· сопоставление результатов с данными об объекте;

· корректировка модели.

В экономическом анализе используются главным образом математические модели, описывающие изучаемое явление или процесс с помощью уравнений, неравенств, функций и других математических средств. Различают модели:

· математические с количественными характеристиками, записанными в виде формул;

· числовые с конкретными числовыми характеристиками;

· логические, записанные с помощью логических выражений;

· графические, выраженные в графических образах.

Модели, реализованные с помощью электронно-вычислительных машин, называют машинными, или электронными.

Экономико-математическая модель должна быть адекватной действительности, должна отражать существенные стороны и свя­зи изучаемого объекта. Отметим принципиальные черты, хара­ктерные для построения экономико-математической модели любого вида. Процесс моделирования можно условно подраз­делить на три этапа:

1) анализ теоретических закономерностей, свойственных изучаемому явлению или процессу, и эмпиричес­ких данных о его структуре и особенностях; на основе такого анализа формируются модели;

2) определение методов, с по­мощью которых можно решить задачу;

3) анализ полученных результатов.

При экономико-математическом моделировании часто воз­никает ситуация, когда изучаемая экономическая система име­ет слишком сложную структуру, не разработаны математичес­кие методы, схемы, которые бы охватывали все основные особенности и

связи этой системы. Такой экономической си­стемой, например, является экономика предприятия в целом, в ее динамике, развитии. Возникает необходимость упрощения изучаемого объекта, исключения и анализа некоторых его второстепенных особенностей с тем, чтобы подвести эту упро­щенную систему под класс уже известных структур, поддающихся математическому описанию и анализу. При этом сте­пень упрощения должна быть такой, чтобы все существенные для данного экономического объекта черты в соответствии с целью исследования были включены в модель.

Важным моментом первого этапа моделирования является четкая формулировка конечной цели построения модели, а так­же определение критерия, по которому будут сравниваться различные варианты решения. В экономическом анализе та­кими критериями могут быть: наибольшая прибыль, наимень­шие издержки производства, максимальная загрузка оборудо­вания, производительность труда и др. В задачах математичес­кого программирования такой критерий отражается целевой функцией. Например, необходимо проанализировать произво­дственную программу выработки продукции с целью выявле­ния резервов повышения прибыли от воздействия структурно­го сдвига в ассортименте. Критерием оптимальности в данном случае при построении экономико-математической модели вы­ступает максимум прибыли. Уравнение целевой функции будет иметь вид:

,

где П_j – прибыль, получаемая от производства единицы продукции j-го вида; х_j – количество производимой продукции (т., шт., ц. и т.д.) j-го вида.

При постановке задач математического программирования обычно предполагается ограниченность ресурсов, которые не­обходимо распределить на производство продукции. Поэтому очень важно определить, какие ресурсы являются для изуча­емого процесса решающими и в то же время лимитирующими, каков их запас. Если все виды производственных ресурсов, к которым относятся сырье, трудовые ресурсы, мощность оборудования и др., используются для выпуска продукции, то необходимо знать расход каждого вида ресурса на единицу продукции.

Все ограничения, отражающие экономический процесс, должны быть непротиворечивыми, т.е. должно существовать хотя бы одно решение задачи, удовлетворяющее всем ограничениям.

В качестве ограничений при построении экономико-мате­матической модели выступает система неравенств, имеющая следующий вид:

, ,

где a_ij – норма расхода i-го производственного ресурса на производ­ство единицы j-го вида продукции; w_i – запасы i-гo вида производственного ресурса на рассматрива­емый период времени.

Объединяя уравнение целевой функции и систему ограниче­ний в единую модель, получим линейную экономико-матема­тическую модель ассортиментной задачи:

,            ;

x_j ³ 0,              .

Не для всякой экономической задачи нужна собственная модель. Некоторые процессы с математической точки зрения однотипны и могут описываться одинаковыми моделями. На­пример, в линейном программировании, теории массового обслуживания и других существуют типовые модели, к кото­рым приводится множество конкретных задач.

Вторым этапом моделирования экономических процессов является выбор наиболее рационального математического ме­тода для решения задачи. Например, для решения задач линей­ного программирования известно много методов: симплекс­ный, потенциалов и др. Лучшей моделью является не самая сложная и не самая похожая на реальное явление или процесс, а та, которая позволяет получить самое рациональное решение и наиболее точные экономические оценки. Излишняя детализа­ция затрудняет построение модели, часто не дает каких-либо преимуществ в анализе экономических взаимосвязей и не обо­гащает выводов. Излишнее укрупнение модели приводит к по­тере существенной экономической информации и иногда даже к неадекватному отражению реальных условий.

Третьим этапом моделирования является всесторонний анализ результата, полученного при изучении экономического явления или процесса. Окончательным критерием достовер­ности и качества модели являются соответствие на практике полученных результатов реальным условиям производства, экономическая содержательность полученных оценок. Если полученные результаты не соответствуют реальным про­изводственным условиям, то необходим экономический анализ причин несоответствия. Такими причинами могут быть недо­статочная достоверность информации,

а также несоответствие используемых математических средств и схем особенностям и сущности изучаемого экономического объекта. После того как причина определена, в модель должны быть внесены соот­ветствующие коррективы, и решение задачи повторяется.

Таким образом, экономико-математическое моделирова­ние работы предприятия должно быть основано на анализе его деятельности и, в свою очередь, обогащать этот анализ ре­зультатами и выводами, полученными после решения соответ­ствующих задач.

Построение, или моделирование, конечной факторной си­стемы для анализируемого экономического показателя хозяй­ственной деятельности может быть осуществлено как форма­льным, так и эвристическим путем на основе качественного анализа сущности экономического явления, отражаемого через данный результативный показатель. Моделирование фактор­ной системы основывается на следующих экономических кри­териях выделения факторов как элементов факторной систе­мы:

· причинности;

· достаточной специфичности;

· самого факта существования;

· возможности учета.

С формальной точки зрения факторы, включаемые в факторную систему, должны быть количественно измеримыми.

В детерминированном моделировании факторных систем можно выделить небольшое число типов конечных факторных систем, наиболее часто встречающихся в анализе хозяйствен­ной деятельности:

1) аддитивные модели:

;

2) мультипликативные модели:

;

3) кратные моде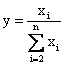ли:

;           ;      ;      или     ,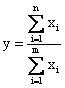

где у – результативный показатель (исходная факторная система), Х_i – факторы (факторные показатели).

Применительно к классу детерминированных факторных систем различают следующие основные приемы моделиро­вания:

1) Метод удлинения факторной системы. Исходная факторная система

.

Если а₁ представить в виде суммы отдельных слагаемых-факторов

а₁ = a₁₁ + а₁₂ + a₁₃  +…a_in,

то

 – это конечная факторная система вида y = åx_i.

2) Метод расширения факторной системы. Исходная факторная система

.

Если и числитель, и знаменатель дроби «расширить» умножением на одно и то же число, то получим новую факторную систему:

,

т.е. мультипликативную модель вида .

3) Метод сокращения факторной системы. Исходная система:

.

Если и числитель, и знаменатель ее разделить на одно и то же число, то получим новую факторную систему (при соблюдении, естественно, правил выделения факторов):

.

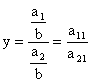В данном случае имеем конечную факторную систему вида .

Таким образом, сложный процесс формирования уровня изучаемого показателя хозяйственной деятельности может быть разложен различными приемами на его

составляющие (факторы) и представлен в виде модели детерминированной факторной системы.

Например, исследуя процесс формирования объема выпускаемой продукции у, можно использовать для анализа такие детерминированные факторные системы:

в статике	в динамике
1) у = x1x2	1) I = i1i2
2) у = х1x3x4	2) I = i1i3i3
3) у = х1x2x3x5x6x7	3) Iy = i1i3i5i6i7

где  у – объем продукции; x₁ – численность работающих; x₂ – производительность труда одного работающего за анализируемый период; x_{3 –} удельный вес рабочих в составе работающих; x₄ – производительность труда одного рабочего за анализи­руемый период; x_{5 –} коэффициент использования рабочих дней; x₆ – коэффициент использования рабочих часов; x_{7 –} средняя часовая производительность труда одного ра­бочего; I_y – общий индекс изменения объема продукции; i_1, i₂, …, i₇ – факторные индексы.

Факторные системы 1 – 3 отражают процесс последовательной детали­зации влияния факторов на изменение объема продукции как обобщающего показателя. Аналогичные модели могут быть построены и для других показателей хозяйственной деятель­ности.

В основе детерминированного моделирования факторной системы лежит возможность построения тождественного пре­образования для исходной формулы экономического пока­зателя по теоретически предполагаемым прямым связям по­следнего с другими показателями-факторами. Детерминиро­ванное моделирование факторных систем – это простое и эф­фективное средство формализации связи экономических по­казателей, оно служит основой для количественной оценки роли отдельных факторов в динамике изменения обобща­ющего показателя.

Детерминированное моделирование факторных систем ограничено длиной факторного поля прямых связей. При не­достаточном уровне знаний о природе прямых связей того или иного показателя хозяйственной деятельности часто необхо­дим иной подход к познанию объективной действительности. Размах количественных изменений экономических показателей можно выяснить только стохастическим анализом массовых эмпирических данных

Стохастический анализ направлен на изучение косвенных связей, т.е. опосредованных факторов (в случае невозмож­ности определения непрерывной цепи

прямой связи). Из этого вытекает важный вывод о соотношении детерминированного и стохастического анализа: так как прямые связи необходимо изучать в первую очередь, то стохастический анализ носит вспомогательный характер. Стохастический анализ выступает в качестве инструмента углубления детерминированного ана­лиза факторов, по которым нельзя построить детерминиро­ванную модель.

Стохастическое моделирование факторных систем взаимосвязей отдельных сторон хозяйственной деятельности опирается на обобщение закономерностей варьирования значений экономических показателей – количественных характеристик факторов и результатов хозяйственной деятельности. Количественные параметры связи выявляются на основе сопоставления значений изучаемых показателей в совокупности хозяйственных объектов или периодов. Таким образом, первой предпосылкой стохастического моделирования является возможность составить совокупность наблюдений, т.е. возможность повторно измерить параметры одного и того же явления в различных условиях.

При детерминированном факторном анализе модель изуча­емого явления не изменяется по хозяйственным объектам и пе­риодам (так как соотношения соответствующих основных ка­тегорий стабильны). При необходимости сравнения резуль­татов деятельности отдельных хозяйств или одного хозяйства в отдельные периоды может возникать лишь вопрос о сопоста­вимости выявленных на основе модели количественных анали­тических результатов. В стохастическом анализе, где сама модель составляется на основе совокупности эмпирических данных, предпосылкой получения реальной модели является совпадение количественных характеристик связей в разрезе всех исходных наблюдений. Это означает, что варьирование значений показателей должно происходить в пределах однозначной определенности качественной стороны явлений, хара­ктеристиками которых являются моделируемые экономичес­кие показатели (в пределах варьирования не должно проис­ходить качественного скачка в характере отражаемого явле­ний.