Пусть на плоскости задана прямоугольная система координат 0 ху . Кривой второго порядка называется линия на плоскости, определяемая уравнением второй степени относительно текущих координат точки М ( х , у , z ). В общем случае это уравнение имеет вид:

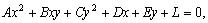
(3.17)

где коэффициенты А , В , С , D , E , L — любые действительные числа, причем хотя бы одно из чисел А , B , С отлично от нуля.

В дальнейшем будут рассмотрены четыре вида кривых второго порядка: окружность, эллипс, гипербола и парабола.

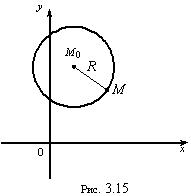
Окружностью называется множество точек на плоскости, расстояние от которых до фиксированной точки М 0( х 0, у 0) постоянно и равно R . Точка М 0 называется центром окружности, а число R — ее радиусом (рис. 3.15).Получим уравнение окружности. Пусть М ( х , у ) есть произвольная точка окружности. Тогда по определению | M 0 М | = R или

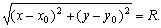
Возводя обе части равенства в квадрат, получим:

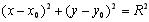
- уравнение окружности с центром в точке М 0( х 0, у 0) и радиусом R .

Если центр окружности совпадает с началом координат, то имеем:

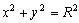
- каноническое уравнение окружности.

Рассмотрим уравнение (3.17) при условии А = С 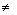0, В = 0. После деления этого уравнения на А и переобозначения коэффициентов получим уравнение:

.

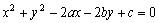
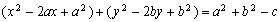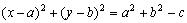Выделим в нем полные квадратыили .Если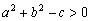, то обозначив 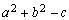через R 2, получим уравнение окружности: 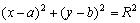с центром в точке М 0( а , b ) радиуса Если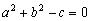, то уравнение: 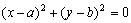задает только точку М 0( а , b ).Если то никакого геометрического образа нет.