Эллипсоидом называется поверхность, задаваемая в некоторой декартовой системе координат уравнением
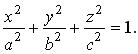
(3.26)
Числа а , b , с называются полуосями эллипсоида.Выясним форму эллипсоида. Поскольку текущие переменные х , у , z входят в уравнение (3.26) в четных степенях, эллипсоид симметричен относительно каждой координатной плоскости. Рассмотрим сечение эллипсоида координатными плоскостями. Плоскость 0 ху имеет уравнение z=0 , поэтому сечение эллипсоида плоскостью 0 ху задается системой уравнений:
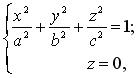
откуда имеем
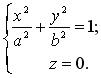
(3.27)
Система (3.27) показывает, что плоскость 0 ху пересекает эллипсоид по эллипсу с полуосями а , b . Аналогично для плоскостей 0 yz , 0 xz соответственно получаем в сечении эллипсы:
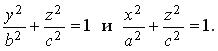
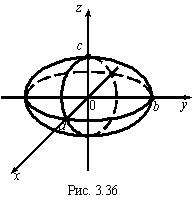
Можно показать, что любая плоскость, параллельная координатной плоскости, пересекает эллипсоид по некоторому эллипсу. Общий вид эллипсоида представлен на рис. 3.36.