Однополостным гиперболоидом называется поверхность, задаваемая в некоторой декартовой системе координат уравнением
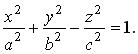
(3.28)
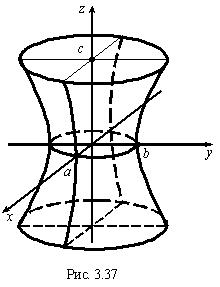
Эта поверхность имеет три плоскости симметрии (координатные плоскости). Выясним, какую форму имеет однополостный гиперболоид, для этого рассмотрим сечения его координатными плоскостями. В плоскости 0 yz получаем:
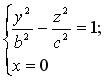
(3.29)
- гиперболу с действительной полуосью b и мнимой полуосью с (в плоскости 0 уz ) (рис. 3.37). Аналогично,
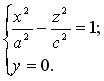
(3.30)
В сечении гиперболоида плоскостью 0 xz также получаем гиперболу с действительной полуосью а и мнимой полуосью с . Пересекая гиперболу плоскостью 0 ху в сечении получаем эллипс:
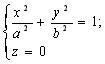
с полуосями а и b . Всякая плоскость, параллельная плоскости 0 ху (она имеет уравнение z = h , h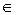 R ), пересекает однополостный гиперболоид по линии:
R ), пересекает однополостный гиперболоид по линии:
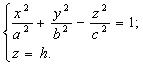
(3.31)
Преобразуем систему (3.31):
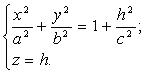
(3.32)
Система (3.32) задает эллипс (рис. 3.37), лежащий в плоскости z = h и имеющий своими полуосями: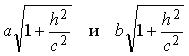 . Однополостный гиперболоид (3.28) не пересекает ось 0 z , она служит осью симметрии для гиперболы (3.29) и гиперболы (3.30) и называется осью гиперболоида (3.28).Уравнение
. Однополостный гиперболоид (3.28) не пересекает ось 0 z , она служит осью симметрии для гиперболы (3.29) и гиперболы (3.30) и называется осью гиперболоида (3.28).Уравнение 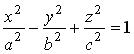 также задает однополостный гиперболоид, но его осью служит 0 у , а для однополостного гиперболоида
также задает однополостный гиперболоид, но его осью служит 0 у , а для однополостного гиперболоида 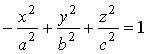 осью является ось 0 х .
осью является ось 0 х .
Двуполостным гиперболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением:
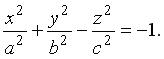
Рассмотрим сечения этой поверхности координатными плоскостями:
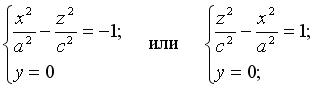
(3.33)
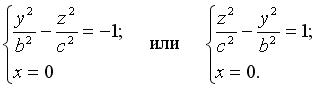
Система (3.33) задает в плоскости 0 xz гиперболу с действительной полуосью с и мнимой полуосью а , система (3.34) — в плоскости 0 уz также гиперболу с действительной полуосью с и мнимой — b . С плоскостью 0 ху двуполостный гиперболоид пересечения не имеет. Действительно, системе: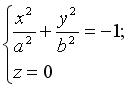 не удовлетворяет ни одна точка пространства.
не удовлетворяет ни одна точка пространства.
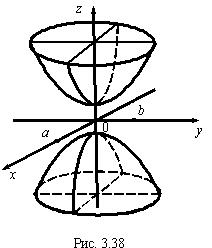 Рассмотрим сечение этого гиперболоида плоскостью, параллельной 0 ху и удаленной от нее на расстояние
Рассмотрим сечение этого гиперболоида плоскостью, параллельной 0 ху и удаленной от нее на расстояние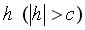 :
: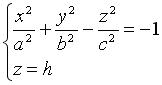 . Из этой системы получаем систему:
. Из этой системы получаем систему: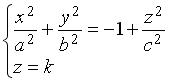 , которая задает эллипс (рис. 3.38) в плоскости z = h с полуосями
, которая задает эллипс (рис. 3.38) в плоскости z = h с полуосями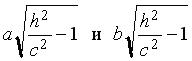 . Ось 0 z является общей осью симметрии для гипербол (3.33) и (3.34) и называется осью двуполостного гиперболоида. Уравнения:
. Ось 0 z является общей осью симметрии для гипербол (3.33) и (3.34) и называется осью двуполостного гиперболоида. Уравнения:
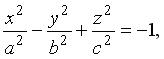
(3.35)
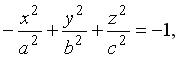
также задают двуполостные гиперболоиды, для (3.35) осью служит 0 у , а для (3.36) — 0 x .