Пример. Составить уравнение линии, расстояния каждой точки которой от точки A (0, — 2) и от прямой 2 y — 5 = 0 относятся как 4 : 5. Решение. Возьмем произвольную точку M ( x, y ) , которая принадлежит искомой линии. Расстояние d между точками A и M равно:

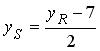
Расстояние 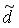от точки M до прямой 2 y — 5 = 0 находим по формуле (3.10):

По условию, следовательно, , т.е.

.

Возведем обе части уравнения в квадрат:

Получили уравнение кривой второго порядка. Для более детального исследования выделим полные квадраты:

следовательно,

Теперь видно, что искомая линия — эллипс, полученный параллельным смещением эллипса:

вдоль оси 0 y на 10 единиц вниз.

Ответ: эллипс

center»>