Пусть U – произвольное множество, «универсум». Мы будем рассматривать теоретико-множественные выражения, которые получаются из символов с помощью операций над множествами, например:
.
Определение
Теоретико-множественное выражение H = H(X1, …, Xm), полученное из подмножеств (X1, …, Xm)ÍU, определяется по индукции:
1) X1, …, Xm, U, Æ – теоретико-множественные выражения;
2) если H – теоретико-множественное выражение, то 
– теоретико-множественное выражение;
3) если H1 и H2 – теоретико-множественные выражения, то (H1ÈH2), (H1ÇH2), (H1H2), (H1DH2) – теоретико-множественные выражения.
Наша цель – научиться решать уравнения
H(X, A1, …, An)= Æ,
где H(X, A1, …, An) – теоретико-множественное выражение, полученное из подмножеств X, A1, …, AnÍU.
Предложение
Для всякого теоретико-множественного выражения H(X, A1, …, An) существуют такие теоретико-множественные выражения
R(A1, …, An), S(A1, …, An), T(A1, …, An),
что для любого XÍU следующие условия равносильны:
1) H(X, A1, …, An)= Æ;
2) R(A1, …, An)È(S(A1, …, An)ÇX)È(T(A1, …, An)Ç 
) = Æ.
Доказательство
Поскольку PQ= PÇ 
и PDQ = (P È Q)(P Ç Q), то можно считать, что H построена с помощью операций PÈ Q, PÇ Q и . Далее применяется индукция по количеству операций в H(X, A1, …, An).
Следствие
В условиях предыдущего предложения, уравнение H(X, A1, …, An)= Æ будет иметь решения тогда и только тогда, когда будут выполнены соотношения:
1. S(A1, …, An)ÇX = Æ,
2. T(A1, …, An)Ç = Æ,
3. R(A1, …, An) = Æ.
Метод решения уравнения
H1(X, A1, …, An)= H2(X, B1, …, Bm).
Здесь A1, …, An и B1, …, Bm – некоторые заданные множества. Обозначим символом 0 пустое множество.
Это уравнение сначала приводят к уравнению
H(X, A1, …, An)= 0,
где
H(X,A1,…, An)= (H1(X, A1, …, An) H2(X, B1, …, Bm)) È ( H2(X, B1, …, Bm) H1(X, A1, …, An)).
Потом для полученного уравнения находим формулы для R, S, T из предыдущего предложения. И, наконец, применим предыдущее следствие. Разберем этот метод решение на следующем примере.
Пример
Рассмотрим, например, уравнение:
AÇX = BÇ
.
Оно равносильно уравнению вида:
= 0.
Следующим шагом решения будет преобразование левой части к объединению пересечений множеств. Это достигается с помощью формул:
PQ = PÇ 
.
После применения этих формул получим:
= 0.
А после применения формул де Моргана приходим к уравнению:
= 0.
С помощью закона дистрибутивности получаем уравнение:
= 0.
Поскольку
и 
,
то это уравнение примет вид:
=0.
Последнее равенство выполняется тогда и только тогда, когда X удовлетворяет системе уравнений:
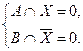
Первое уравнение равносильно включению 
, а второе – 
. Отсюда вытекает следующий ответ:
.