Посмотрим, как по ![]() -диаграмме определяется работа изменения объёма. Допустим, что рабочее тело произвольной массой
-диаграмме определяется работа изменения объёма. Допустим, что рабочее тело произвольной массой ![]() с давлением р заключено в цилиндре с поршнем (рис. 6.2).
с давлением р заключено в цилиндре с поршнем (рис. 6.2).

Рис. 6.2. PV-диаграмма для определения работы изменения объема
Если под действием каких-либо сил тело расширяется и поршень передвигается на бесконечно малое расстояние ![]() , преодолевая внешние силы, то рабочим телом будет совершаться бесконечно малая работа
, преодолевая внешние силы, то рабочим телом будет совершаться бесконечно малая работа ![]() . Элементарная работа, совершенная рабочим телом, будет равна:
. Элементарная работа, совершенная рабочим телом, будет равна:
![]() ,
,
где: р – давление, действующее на поршень; А – площадь поршня.
Поскольку произведение ![]() равно элементарному изменению объема газа
равно элементарному изменению объема газа ![]() , то можно записать:
, то можно записать:
![]() .
.
Деля левую и правую часть последнего выражения на массу газа ![]() , найдем элементарную удельную работу, совершенную 1 кг газа
, найдем элементарную удельную работу, совершенную 1 кг газа
![]() . (6.5)
. (6.5)
На ![]() -диаграмме (см. рис. 6.2) эта работа изображена узкой заштрихованной площадкой. Интегрируя выражение (6.5) в пределах от
-диаграмме (см. рис. 6.2) эта работа изображена узкой заштрихованной площадкой. Интегрируя выражение (6.5) в пределах от ![]() до
до ![]() , получим выражение для определения удельной работы всего процесса 1 – 2:
, получим выражение для определения удельной работы всего процесса 1 – 2:
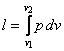 . (6.6)
. (6.6)
Из уравнения (6.6) видно, что условием совершения удельной работы является изменение удельного объёма рабочего тела. Нетрудно убедиться в том, что изменение давления и температуры рабочего тела, может происходить без совершения такой работы (пример с баллоном, который нагревается).
Интеграл в уравнении изображает площадь диаграммы 1234 (рис. 6.2), поэтому можно сделать вывод, что площадь на ![]() -диаграмме, заключённая между линией процесса, осью абсцисс и крайними ординатами этой линии и изображает удельную
-диаграмме, заключённая между линией процесса, осью абсцисс и крайними ординатами этой линии и изображает удельную
работу изменения объёма газа всего процесса. Работа изменения объёма зависит от вида линии процесса.
Действительно, из рис. 6.2 видно, что изображаемая площадью под кривой процесса 1 – 2 работа (l) зависит от процесса: в процессе 1 – а – 2 она больше, чем в процессе 1 – b – 2 или 1 – с – 2. Так, например, если процесс изотермический, то работа равна:
![]() .
.
В изобарном процессе работа равна:
![]() .
.
Следовательно, она является функцией процесса.