Понятие энтропии введем следующим образом. Пусть имеется источник теплоты с постоянной температурой Т и рабочее тело той же температуры Т, к которому от источника обратимо подводится количество теплоты dQ. Необходимо отыскать величину, которая характеризовала бы изменение состояния рабочего тела. Поскольку изменяются только температура и количество теплоты, причем с повышением Т воздействие dQ на состояние рабочего тела уменьшается, то такой величиной может быть только соотношение:
![]() .
.
Величина S была названа Клазиусом энтропией. Если же в рассматриваемом примере температура источника (Ти) будет выше температуры рабочего тела Т, то переход теплоты обратно от рабочего тела к источнику окажется невозможным, как противоречащий второму началу термодинамики, т.е. мы будем иметь дело с необратимым процессом. Тогда:
![]() ,
,
и общее выражение второго закона термодинамики для обратимых и необратимых процессов будет иметь вид:
![]() .
.
Если же система (рабочее тело) изолирована в тепловом отношении, т.е. не получает и не отдает теплоту (dQ = 0), то ![]() . Энтропия изолированных систем при обратимых процессах постоянна, а при необратимых возрастает, уменьшаться она не может. Поскольку все реальные процессы необратимы, второй закон называют законом возрастания энтропии.
. Энтропия изолированных систем при обратимых процессах постоянна, а при необратимых возрастает, уменьшаться она не может. Поскольку все реальные процессы необратимы, второй закон называют законом возрастания энтропии.
Понятие энтропии позволяет ввести очень удобную для термодинамических процессов и циклов диаграмму состояний, в которой по оси абсцисс откладывают значение энтропии, а по оси ординат – абсолютную температуру. В T-S-диаграмме состояние рабочего тела изображается точками, термодинамические процессы линиями, а теплота, участвующая в процессе, площадью под линией процесса.
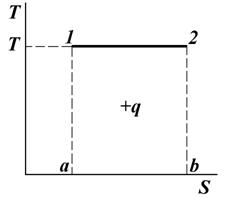
Рис. 7.1. График изотермического процесса
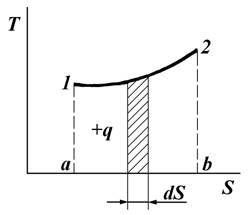
Рис. 7.2. График процесса с переменной температурой
В процессе при T = const (рис. 7.1) имеем:
![]() или
или ![]() .
.
На диаграмме отрезок 1 – а равен Т, а отрезок а – b разности энтропий (S2 – S1). Тогда произведение этих отрезков, равное площади прямоугольника 1 – 2 – а – b – 1, определяет теплоту процесса 1 – 2.
В процессе с переменной температурой (рис. 7.2) теплоту, участвующую в процессе, также можно изобразить графически под линией процесса 1 — 2. Если процесс 1 — 2 разбить на бесконечно большое множество бесконечно малых отрезков, в пределах которых Т можно считать неизменной, то для элементарного количества теплоты имеем: ![]() . Для определения всего количества теплоты, участвующей в процессе 1 — 2, следует проинтегрировать последнее уравнение:
. Для определения всего количества теплоты, участвующей в процессе 1 — 2, следует проинтегрировать последнее уравнение:
![]() .
.
Отметим, что иногда T-S-диаграмму называют тепловой.