Если соединяемые элементы подвержены изгибу (случай несимметричного нагружения), то нагрузка между одиночными заклепочными соединениями распределяется неравномерно. В этом случае расчет групповых соединений сводится обычно к определению наиболее нагруженной заклепки и оценке ее прочности.

Рассмотрим соединение, содержащее n заклепок одинакового диаметра d под действием силы F (рис. 3.10, а). Примем для упрощения, что трение между соединяемыми деталями отсутствует и вся внешняя нагрузка передается через заклепки. Предположим, что деформации (изгиб, сдвиг) соединяемых деталей малы по сравнению с деформациями стержней заклепок. При этих допущениях можно полагать, что возможный взаимный поворот соединяемых деталей (листов) произойдет вокруг точки С (рис. 3.10, б) – центра масс поперечных сечений стержней заклепок. Следовательно, точку С можно использовать в качестве центра приведения внешней силы.

В результате приведения внецентренной силы F в точку С (рис. 3.10) задача расчета группового соединения сводится к определению наиболее нагруженной заклепки от действия центральной силы F (или ее осевых составляющих) и вращающего момента

T = FL,

где L – расстояние от точки С до линии действия силы F.

Если соединение подвержено действию нескольких сил , то в результате приведения их к точке С оно будет нагружено главным вектором и главным моментом от этих сил.

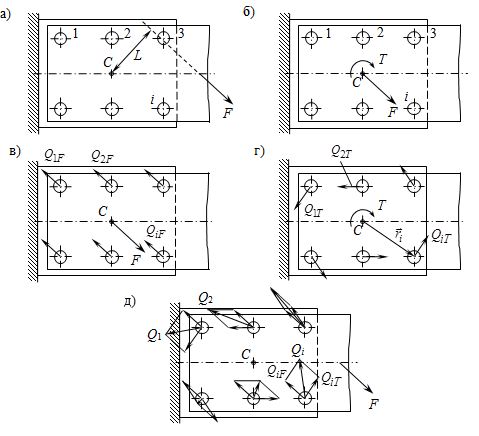
Рис. 3.10. Расчетные схемы для соединения при действии несимметричной нагрузки

При упругой деформации заклепок действие каждого силового фактора (F и Т) можно рассматривать независимо. Тогда сила, приходящаяся на каждую заклепку от силы F (рис. 3.10, в), будет равна

,

где  – номер заклепки.

Момент (Т) вызывает в каждой заклепке реактивную силу, направленную перпендикулярно к радиусу-вектору , проведенному из точки С в центр сечения -й заклепки (рис. 3.10, г). Эта сила пропорциональна перемещению сечения в результате деформации сдвига. Так как сдвиги сечений заклепок прямо пропорциональны их расстояниям  до центра масс, то можно записать:

;   .

Откуда

;    ;    …;    .   (3.6)

Если учесть, что внешний момент (Т) уравновешивается моментами от сил, действующих на заклепки, т.е.

,    (3.7)

то после подстановки в это уравнение (3.7) равенства (3.6) получим выражение для силы, действующей на первую заклепку:

,

или выражение для силы, действующей на -ю заклепку:

.

Сила, действующая на наиболее нагруженную заклепку, равна:

,

откуда модуль этой силы вычисляется следующим образом:

,

где  – угол между векторами сил  и  (рис. 3.10, д).

Диаметр заклепки при известных значении  и ее материале находится по формуле (3.2).