Адиабатным называется процесс изменения состояния рабочего тела без отвода и подвода теплоты.
Уравнение адиабатного процесса:
pvk = const,
где k = cp/cv – показатель адиабаты.
Графическое изображение адиабатного процесса в pv- и TS-диаграммах показано на рис. 8.4.
Заметим, что адиабата идет круче изотермы, так как ![]() .
.
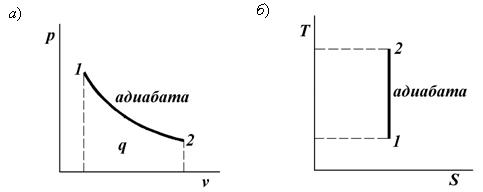
Рис. 8.4. Графическое изображение адиабатного процесса в pv- и TS-диаграммах
Связь между параметрами газа в адиабатном процессе найдем следующим образом. Поскольку ![]() , то для двух точек процесса имеем:
, то для двух точек процесса имеем:
![]()
или
![]() , (8.2)
, (8.2)
что равносильно
![]() . (8.3)
. (8.3)
Для того чтобы определить зависимость между удельным объемом (v) и температурой (T), запишем уравнения состояния для двух точек:
![]() ,
,
и, поделив их друг на друга, получим:
![]() . (8.4)
. (8.4)
С учетом формулы (8.2) имеем:
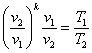 ,
,
откуда
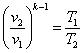 .
.
Связь между давлением (р) и температурой (Т) найдем путем совместного решения уравнений (8.3) и (8.4), т.е. получим:
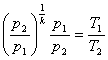
или
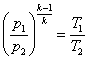 .
.
Изменение внутренней энергии газа в адиабатном процессе находится по формулам:
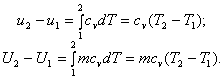
Для вывода формулы по расчету работы изменения объема воспользуемся первым законом термодинамики:
![]() .
.
Так как в адиабатном процессе ![]() , то
, то ![]() . Следовательно:
. Следовательно:
![]() . (8.5)
. (8.5)
Разделим левую и правую часть уравнения Майера
![]()
на ![]() . С учетом того, что
. С учетом того, что ![]() , получим:
, получим:
![]()
откуда
![]() . (8.6)
. (8.6)
Тогда имеем:
![]() .
.
Связь между работой изменения объема и работой изменения давления найдем с помощью формулы по определению показателя адиабаты. После умножения числителя и знаменателя уравнения ![]() на (
на (![]() ) получим:
) получим:
![]() .
.
Сравнивая последнее выражение с выражением (8.5) видим, что знаменатель дроби равен работе изменения объема. Исходя из того, что ![]() , на основании формулы (6.11) и, учитывая, что в адиабатном процессе
, на основании формулы (6.11) и, учитывая, что в адиабатном процессе ![]() , имеем:
, имеем:
![]() .
.
Следовательно:
![]() .
.