У косозубых колес зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол β (рис. 9.13). Профиль косого зуба в нормальном сечении ![]() совпадает с профилем прямого зуба. Модуль в этом сечении должен быть стандартным.
совпадает с профилем прямого зуба. Модуль в этом сечении должен быть стандартным.
В торцовом сечении ![]() косозубого колеса изменяются в зависимости от угла β:
косозубого колеса изменяются в зависимости от угла β:
· окружной шаг
![]() ;
;
· окружной модуль
![]() ;
;
· делительный диаметр
![]() или
или ![]() .
.
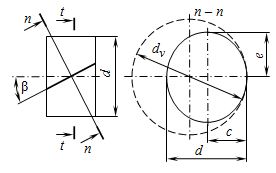
Рис. 9.13. К определению эквивалентных параметров косозубого колеса
Прочность зуба определяют его размеры и форма в нормальном сечении. Форму косого зуба в нормальном сечении принято определять через параметры эквивалентного прямозубого колеса (рис. 9.13).
Нормальное к зубу сечение образует эллипс с полуосями:
![]() ;
; ![]() ,
,
где ![]() .
.
В зацеплении участвуют зубья, расположенные на малой оси эллипса, так как второе колесо находится на расстоянии ![]() . Радиус кривизны эллипса на малой оси (см. геометрию эллипса) определяется из выражения:
. Радиус кривизны эллипса на малой оси (см. геометрию эллипса) определяется из выражения:
![]() .
.
В соответствии с этим эквивалентное колесо будет иметь следующие параметры:
· эквивалентный диаметр
![]() ;
;
· эквивалентное число зубьев
![]() .
.
Эквивалентные параметры используются для распространения расчетов на прочность цилиндрических прямозубых передач на цилиндрические косозубые передачи. Увеличение эквивалентных параметров с увеличением угла β является одной из причин повышения прочности косозубых передач. Вследствие наклона зубьев получается колесо как бы больших размеров или при той же нагрузке уменьшаются габариты передачи.