При расчете червячной передачи на прочность расчетная нагрузка или расчетный момент определяются умножением соответствующих номинальных величин на коэффициент нагрузки (
).
Коэффициент нагрузки для червячных передач определяют как произведение коэффициента концентрации нагрузки (
) на динамический (скоростной) коэффициент (
).
Концентрация нагрузки по длине зубьев в основном вызвана деформацией (прогибом) червяка вследствие значительного расстояния между опорами и ограниченного диаметра червяка для уменьшения потерь на трение.
При проектном расчете на контактную выносливость коэффициент нагрузки определяют по формуле^
,
где 
– теоретический (начальный) коэффициент концентрации нагрузки.
При проектном расчете начальный коэффициент концентрации нагрузки () принимают по рис. 11.6.
Теоретический коэффициент концентрации нагрузки в условиях отсутствия приработки определяют по формуле:
, (11.5)
где 
– коэффициент деформации червяка. Коэффициент деформации червяка определяется в зависимости от 
и 
по табл. 11.7.
При проектном расчете начальный коэффициент концентрации нагрузки () можно также определить по формуле (11.5), предварительно приняв коэффициент диаметра червяка 
.
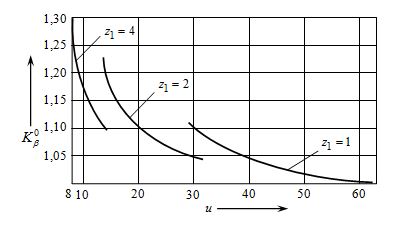
Рис. 11.6. График для определения начального коэффициента концентрации нагрузки
При проверочном расчете на контактную выносливость и на выносливость при изгибе коэффициент нагрузки уточняется по формуле:
, (11.6)
где 
– коэффициент неравномерности (концентрации) нагрузки; 
– динамический (скоростной) коэффициент.
Таблица 11.7 Коэффициент деформации червяка 
|
|
Значения коэффициента деформации |
||||||||
|
7,1 |
8 |
9 |
10 |
11 |
12,5 |
14 |
16 |
20 |
|
|
1 |
57 |
72 |
89 |
108 |
127 |
157 |
190 |
225 |
248 |
|
2 |
45 |
57 |
71 |
86 |
102 |
125 |
152 |
171 |
197 |
|
3 |
40 |
51 |
61 |
76 |
89 |
110 |
134 |
148 |
170 |
|
4 |
37 |
47 |
58 |
70 |
82 |
101 |
123 |
137 |
157 |
при заданном значении 
Зубья червячного колеса обладают способностью прирабатываться. При постоянной нагрузке происходит полная приработка, и распределение нагрузки выравнивается. При переменной нагрузке происходит частичная приработка, и зубья получают естественную бочкообразность. Поэтому концентрацию нагрузки необходимо учитывать по отношению к избыточному моменту 
. Коэффициент концентрации нагрузки в данном случае определяется по формуле:
,
где 
– вспомогательный коэффициент, зависящий от характера изменения нагрузки. Он определяется как отношение средневзвешенного момента (
) к максимальному длительно действующему моменту (
):
или 
;
; 
,
где 
– момент при 
-м режиме работы; 
– частота вращения при -м режиме работы; 
– время работы при -м режиме.
В расчетах, когда не требуется особая точность, можно принимать:
· при постоянной нагрузке 
;
· при незначительных колебаниях нагрузки 
;
· при значительных колебаниях нагрузки 
.
При постоянной нагрузке коэффициент концентрации нагрузки равен единице (
).
Динамический (скоростной) коэффициент () определяется в зависимости от точности изготовления передачи и скорости скольжения (табл. 11.8). Скорость скольжения должна быть уточнена по формуле (11.4).
Таблица 11.8 Коэффициент динамической нагрузки 
|
Степень точности |
Скорость скольжения |
|||
|
до 0,5 |
св. 1,5 до 3 |
св. 3 до 7,5 |
св. 7,5 до 12 |
|
|
6 |
– |
– |
1,0 |
1,1 |
|
7 |
1,00 |
1,00 |
1,1 |
1,2 |
|
8 |
1,15 |
1,25 |
1,4 |
– |
|
9 |
1,25 |
– |
– |
– |
|
Примечание: Для силовых передач предназначаются степени точности 5 – 9; для редукторов общего назначения обычно применяют 7– 8 степени точности. |
||||
Обычно 
. При точном изготовлении передачи (площадь контакта составляет не менее 75 % от номинальной) и окружной скорости на делительном диаметре червячного колеса 
м/с принимают 
.