Принимают, что для материала ремней справедлив закон Гука. Тогда после приложения полезной нагрузки сумма натяжений ветвей остается постоянной. Действие центробежной силы в упрощенных расчетах не учитывают, так как она уравновешивается в ремне и может вызвать лишь разгрузку валов.
Если ветви ремней параллельны (![]() ) сила на валы (
) сила на валы (![]() ) равна двойному начальному натяжению ремня:
) равна двойному начальному натяжению ремня:
![]() .
.
Если ветви ремней не параллельны (![]() ) сила на валы (
) сила на валы (![]() ) определяется из треугольника ОАВ (рис. 15.7) по теореме косинусов:
) определяется из треугольника ОАВ (рис. 15.7) по теореме косинусов:
![]() . (15.24)
. (15.24)
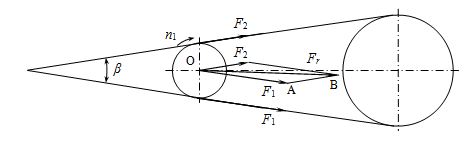
Рис. 15.7. Силы, действующие на валы
Подставляя в выражение (15.24) значения натяжений ![]() и
и ![]() , определяемые по формулам (15.19), получим приближенное выражение для определения силы на валы:
, определяемые по формулам (15.19), получим приближенное выражение для определения силы на валы:
![]() . (15.25)
. (15.25)
Вторым слагаемым под корнем выражения (15.25) можно пренебречь в виду его малости по сравнению с первым слагаемым, поэтому имеем:
![]() . (15.26)
. (15.26)
Приближение (15.26) тем справедливее, чем ближе передаточное число к единице. Нагрузку на валы можно также определить через угол обхвата (![]() ):
):
![]() . (15.27)
. (15.27)
Зависимости (15.26) и (15.27) используются для расчета нагрузки на валы при автоматическом регулировании натяжения ремня.
В передачах без регулирования натяжения его обычно устанавливают с запасом, и оно сохраняется до вытягивания ремня. Поэтому при расчете нагрузки на валы в данном случае расчетное начальное натяжение (![]() ) и напряжение
) и напряжение ![]() увеличивают в 1,5 раза:
увеличивают в 1,5 раза:
![]() , (15.28)
, (15.28)
где ![]() – соответственно ширина и толщина плоского ремня;
– соответственно ширина и толщина плоского ремня; ![]() – площадь поперечного сечения клинового ремня;
– площадь поперечного сечения клинового ремня; ![]() – число клиновых ремней.
– число клиновых ремней.