Пример 9.1
Найти максимально допустимое давление сжатия в идеальном одноступенчатом воздушном компрессоре (р2), если температура самовоспламенения смазочного масла tм = 270° С, температура наружного воздуха, поступающего в компрессор, tв = 27°С (начальное давление воздуха р1 = 0,1 МПа), сжатие происходит по адиабате (k = 1,4).
Решение
Максимально допустимую температуру воздуха в конце сжатия принимаем равной температуре самовоспламенения масла:
T2 = tм + 273 = 270 + 273 = 543 К.
Температуру воздуха в начале сжатия примем равной температуре наружного воздуха Тв = 300 К. Максимально допустимое конечное давление воздуха равно:
![]() = 0,1·106·(543 / 300)1,4/(1,4-1) = 0,798 МПа.
= 0,1·106·(543 / 300)1,4/(1,4-1) = 0,798 МПа.
Из этого примера следует, что для бескомпрессорных дизелей, требующих применения пускового воздуха давлением порядка 3 МПа, одноступенчатый пусковой компрессор непригоден.
Пример 9.2
Объемная подача идеального одноступенчатого воздушного компрессора составляет 0,2 м3/с при температуре всасывания 27° С и давлении 0,1 МПа. Давление сжатого воздуха 0,8 МПа. Найти температуру воздуха и объемную подачу компрессора (по конечным параметрам воздуха) в конце сжатия и мощность, затрачиваемую на получение сжатого воздуха, в трех вариантах:
1) при сжатии по изотерме;
2) по адиабате (k = 1,4);
3) и по политропе (п = 1,2).
Решение
1) При изотермическом сжатии
Абсолютная температура равна:
T2 = T1= 27 + 273 = 300 К.
Объемная подача по конечным параметрам равна:
![]() = 0,2·(0,1·106 / 0,8·106) = 0,025 м3/с.
= 0,2·(0,1·106 / 0,8·106) = 0,025 м3/с.
Последнее выражение получено с учетом того, что ![]() .
.
Мощность при изотермическом сжатии определим по уравнению (9.6), с учетом формул (9.2), (9.7) и того, что ![]() :
:
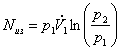 /1000=0,1·106·0,2·ln 8 / 1000=41,5 кВт.
/1000=0,1·106·0,2·ln 8 / 1000=41,5 кВт.
1) При адиабатном сжатии
Конечная температура воздуха равна:
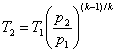 = 300·8(1,4-1)/1,4 = 544 К.
= 300·8(1,4-1)/1,4 = 544 К.
Объемная подача по конечным параметрам:
![]() = 0,2·(1 / 8)1/1,4 = 0,045 м3/с.
= 0,2·(1 / 8)1/1,4 = 0,045 м3/с.
Мощность при адиабатном сжатии определим из совместного рассмотрения уравнений (9.6), (9.3) и (9.7). Так же, как и в первом случае, учитываем, что![]() . Получим:
. Получим:
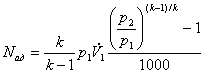 = 1,4 / (1,4 — 1)·0,1·106 ·0,2·[8(1,4-1)/1,4 - 1] / 1000 = 56,7 кВт.
= 1,4 / (1,4 — 1)·0,1·106 ·0,2·[8(1,4-1)/1,4 - 1] / 1000 = 56,7 кВт.
2) При политропном сжатии
Конечная температура воздуха:
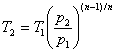 = 300·8(1,2-1)/1,2 = 368 К.
= 300·8(1,2-1)/1,2 = 368 К.
Объемная подача по конечным параметрам:
![]() = 0,2·(1/8)1/1,2 = 0,033 м3/с.
= 0,2·(1/8)1/1,2 = 0,033 м3/с.
Выражение для определения мощности при политропном сжатии определяется аналогично, как и для случая адиабатного сжатия. Только вместо уравнения (9.3) будем использовать выражение (9.5). Получим:
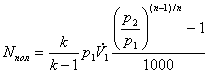 = 1,4 / (1,4 — 1)·0,1·106 ·0,2·[8(1,2-1)/1,2 - 1] / 1000 = 49,8 кВт.
= 1,4 / (1,4 — 1)·0,1·106 ·0,2·[8(1,2-1)/1,2 - 1] / 1000 = 49,8 кВт.
Пример 9.3
Исследовать термодинамический цикл ДВС со смешанным подводом теплоты по следующим данным: ра = 0,1 МПа; ta = 27° С; cv = 0,72 кДж/(кг К); k = 1,4; ![]() +
+ ![]() = 1340 кДж/кг;
= 1340 кДж/кг; ![]() = 5,5 МПа и ε = 15. Рабочее тело – воздух, рассматриваемый как идеальный газ. Масса воздуха 1 кг.
= 5,5 МПа и ε = 15. Рабочее тело – воздух, рассматриваемый как идеальный газ. Масса воздуха 1 кг.
Решение
Находим параметры в характерных точках цикла (см. рис. 9.14).:
В точке а – начале сжатия
![]() .
.
Для воздуха R = 287,1 Дж/(кг·К);
Та = 273 + ta = 273 + 27 = 300 К,
поэтому
va = 287,1 · 300 / (0,1·106) = 0,861 м3/кг;
В точке с – конце сжатия
![]() = 0,861 / 15 = 0,0573 м3/кг;
= 0,861 / 15 = 0,0573 м3/кг;
![]() ,
,
откуда
![]() = 0,1·151,4 = 4,43 МПа;
= 0,1·151,4 = 4,43 МПа;
![]() = 4,43·106 ·0,0573 / 287,1 = 883 К
= 4,43·106 ·0,0573 / 287,1 = 883 К
или
tc = 610 °С.
В точке ![]() – конце подвода теплоты при постоянном объеме
– конце подвода теплоты при постоянном объеме
степень повышения давления:
![]() = 5,5 / 4,43 = 1,242;
= 5,5 / 4,43 = 1,242;
![]() = 883 · 1,242 = 1097 К
= 883 · 1,242 = 1097 К
или
![]() = 824 °С;
= 824 °С;
![]()
![]() = 0,0573 м3/кг.
= 0,0573 м3/кг.
В точке z – конце подвода теплоты при постоянном давлении
Предварительно вычисляем ![]() , так как
, так как ![]() +
+ ![]() = 1340 кДж/кг, то сначала подсчитаем
= 1340 кДж/кг, то сначала подсчитаем ![]() :
:
![]() = 0,72·106·(1097 – 883) = 154 кДж/кг,
= 0,72·106·(1097 – 883) = 154 кДж/кг,
поэтому
![]() = 1340 – 154 = 1180 кДж/кг.
= 1340 – 154 = 1180 кДж/кг.
Температуру ![]() определяем из уравнения:
определяем из уравнения:
![]() ,
,
отсюда
![]() .
.
Находим предварительно cp:
![]() = 1,4·072·103 = 1,01 кДж/(кг·К).
= 1,4·072·103 = 1,01 кДж/(кг·К).
Подставляя значение cp, определяем:
![]() = 1186 / 1,01 + 1097 = 2274 К
= 1186 / 1,01 + 1097 = 2274 К
или
tz = 2274 — 273 = 2001 °С.
Найдем vz. Сначала подсчитаем степень предварительного расширения:
![]() = 2274 / 1097 = 2,07.
= 2274 / 1097 = 2,07.
Теперь вычисляем vz:
![]() = 2,07 · 0,0573 = 0,118 м3/кг.
= 2,07 · 0,0573 = 0,118 м3/кг.
В точке е – конце адиабатного расширения
![]() = 0,861 м3/кг;
= 0,861 м3/кг;
находим
![]() = 300 · 1,242 · 2,071,4 = 1034 К
= 300 · 1,242 · 2,071,4 = 1034 К
или
tе = 1034 – 273 = 761 °С.
Давление в искомой точке цикла:
![]() = 0,1 · 1,242 · 2,071,4 = 0,344 МПа.
= 0,1 · 1,242 · 2,071,4 = 0,344 МПа.
Определим термический КПД цикла по уравнению (9.9):
![]() =
=
= 0,605 (60,5 %).