Для записи информации о количестве объектов материального мира используются числа, которые разделяются по определенным признакам, например по групповому признаку (рис. 3.4), когда в каждую группу входят числа, обладающие определенными свойствами.

Числа записываются с использованием особых знаковых систем, которые называются системами счисления, в них числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Можно выделить два основных класса, на которые разделяются системы счисления – позиционные и непозиционные.

В непозиционных системах количественное значение символа определяется только его изображением и не зависит от его места (позиции) в числе. Например, в римской системе счисления десятичное число 27 представляется:

XXVII = 10 + 10 + 5 + 1 + 1,

другими словами количественное значение символа определяется либо суммой значений символов (как в числе 27), либо их разностью (как в числе 9 – IX). Значение числа зависит от места символа по отношению к другому символу, то есть значение символа не однозначно. В непозиционных системах счисления не представляются дробные и отрицательные числа.

Система счисления называется позиционной, если значение числа в ней определяется как цифрами, принятыми в системе, так и положением (позицией) этих цифр в числе. Закономерность построения позиционных чисел имеет простое математическое представление.

Введем следующие обозначения:

q – основание системы счисления. Основание системы это целое положительное число, большее 1 и равное максимальному количеству различных символов, употребляемых в данной системе счисления. В частности, для десятичной системы счисления q = 10;

a_i – любая цифра из множества цифр, принятых в данной системе счисления (в случае десятичной системы a_i – любая цифра из множества 0, 1, 2,…, 9);

i – буквенный индекс, который обозначает номер позиции, занимаемой цифрой.

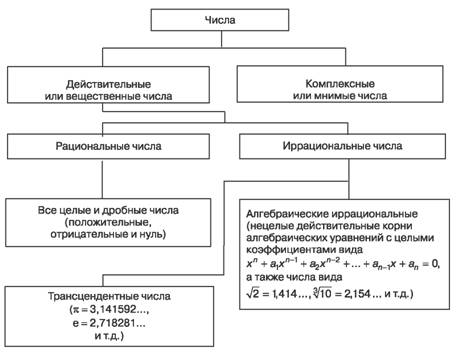
Рис. 3.4. Классификация чисел по групповому признаку

Позицию для целых чисел будем условно обозначать номерами 0, 1, 2, …, n, а позиции в правильных дробях – номерами со знаком «минус»: -1, -2, …, -m. Тогда любое число А в произвольной позиционной системе счисления с основанием q может быть записано следующим образом:

где a_i – удовлетворяет неравенству

и принимает в этом диапазоне только целые значения.

Величину a_i будем называть весом i-го разряда. Тогда число A в десятичной системе счисления будет иметь вид:

A = a_n 10ⁿ + a_n-1 10^n-1 + … + a₀ 10⁰ + a_-1 10^-1 + …+ a_-m 10^-m

Для десятичной системы счисления понятие веса разряда соответствует общепринятым названиям позиций – единицы, десятки, сотни, десятые доли и т.д.

Пример

Если дано число 345, то ясно, что в этом числе 5 единиц, 4 десятка и 3 сотни.

Формулу (3.1) будем называть общей формулой записи числа в позиционной системе счисления с произвольным целым основанием q.

Большинство современных компьютеров работает в двоичной системе счисления (q = 2). Согласно соотношению (3.2) для записи двоичного числа достаточно использовать только две цифры 0 и 1.

Двоичная система, в которой работает ЭВМ, не удобна для восприятия человеком. Большое количество разрядов двоичного числа по сравнению с соответствующим десятичным, однообразное чередование единиц и нулей является источником ошибок и затрудняет чтение двоичного числа. Поэтому для удобства записи двоичных чисел необходима такая система счисления, которая, с одной стороны, сохраняла бы свойства двоичной, а с другой – в написании была бы близка к десятичной. Такими свойствами обладают системы счисления с основанием 2ⁿ, например, 2³ – восьмеричная и 2⁴ – шестнадцатеричная системы счисления.

Эти системы удобны тем, что в них обеспечивается чрезвычайно легкий (в уме) перевод из двоичной системы и в тоже время сохраняется привычный для человека вид числа.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Являются ли понятия «информация» и «данные» синонимами? Дайте определение тому и другому понятию.

2. Какие типы информации вам известны?

3. Верно ли высказывание: «информация в компьютере всегда представлена в бинарном виде»?

4. Какие проблемы могут возникнуть при сохранении результатов некоторых арифметических операций?

5. Как решается проблема наличия разных алфавитов в разных языках при кодировании и хранении символьной информации?

6. Что такое ASCII?

7. Зачем нужны служебные данные?