Дифференциальное уравнение теплопроводности при стационарном режиме без внутренних источников теплоты имеет вид:

Для решения конкретной задачи к этому уравнению надо присовокупить соответствующие граничные условия. Рассмотрим несколько простейших случаев определения стационарного поля температур в телах различной формы.

Плоская стенка

Рассмотрим неограниченную тонкую стенку толщиной  (рис. 10.5).

Рис. 10.5. Схема для определения стационарного поля температур в телах с плоской стенкой

Пусть на поверхностях стенки поддерживаются соответственно температуры  и . Если  и  не зависят от z и y, то очевидно, искомое температурное поле тоже не будет зависеть от этих координат и тогда:

.                  (10.2)

При отыскании распределения поля температур используем граничные условия:

             при

             при

Представим выражение (10.2) в виде:

.

После первого интегрирования имеем:

        или        .

После второго интегрирования имеем:

.

Постоянные  и  определим из граничных условий. Из первого граничного условия имеем:

;

из второго граничного условия определим константу :

,

откуда

.

Таким образом, решением уравнения (10.2) будет выражение:

,

т.е. функция T(x) линейно зависит от x.

Найдем плотность теплового потока. Согласно закону Фурье:

или в данном случае:

.

Определим количество теплоты потока через стенку в единицу времени:

,

где F – площадь стенки.

Теперь определим плотность теплового потока через трехслойную стенку (рис. 10.6).

Рис. 10.6. Определение плотности теплового потока через трехслойную стенку

Для каждого слоя можно записать следующие выражения:

для первого слоя

;                        (10.3)

для второго слоя

;                (10.4)

для третьего слоя

.                   (10.5)

Из уравнений (10.3) – (10.5) можно найти термическое сопротивление трехслойной стенки. Для этого сначала определим местные температурные напоры на каждой стенке:

.

Почленно сложив эти уравнения, получим:

,

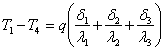откуда

.

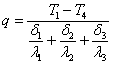На основании последнего выражения для многослойной стенки получим:

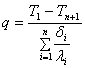,                      (10.6)

где n – количество слоев.

С вводом обозначения

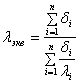,                     (10.7)

где  – эквивалентная теплопроводность, выражение (10.6) можно представить в виде:

.

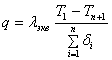Цилиндрическая стенка

Запишем дифференциальное уравнение теплопроводности в цилиндрической системе координат. Для этого используем известные соотношения, связывающие декартовы и цилиндрические координаты (рис. 10.7):  

Тогда

.

Рассмотрим одномерный процесс теплопроводности в бесконечной цилиндрической стенке (рис. 10.8). Предположим, что на внутренней и внешней полостях стенки, температура не зависит от угла . Тогда получим:

.                   (10.8)

Зададим граничные условия задачи:

            при            ;

            при            .

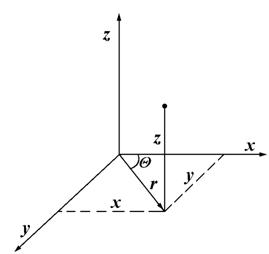
Рис. 10.7. Переход от декартовых к цилиндрическим координатам

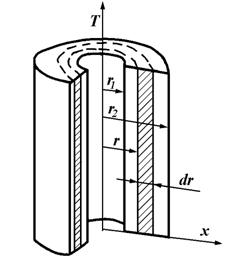
Рис. 10.8. Одномерный процесс теплопроводности в бесконечной цилиндрической стенке

Приведем уравнение (10.8) к виду:

откуда

.

После первого интегрирования получим:

   или   .

После второго интегрирования имеем:

.                       (10.9)

Постоянные интегрирования определим из граничных условий:

при

;                       10.10)

при

.                    (10.11)

Вычитая из уравнения(10.11) выражение (10.10) получим:

,

следовательно,

.

Постоянную  найдем из уравнения (10.10):

.

Подставляя выражения для  и  в уравнение (10.9), найдем:

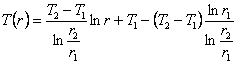
или

.

Из последнего выражения видно, что искомое распределение температуры по толщине цилиндрической стенки логарифмически зависит от координаты r.

Плотность теплового потока  определим из закона Фурье:

.

Количество теплоты, проходящее сквозь цилиндрическую стенку, через единицу длины:

.

Используя последнюю формулу можно определить количество теплоты, проходящее сквозь многослойную цилиндрическую стенку:

,

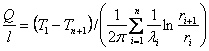где n – количество слоев.