Прежде чем перейти к описанию гетерогенных равновесий, нам необходимо ввести некоторые понятия, используемые при рассмотрении гомогенных равновесий. Для упрощения изложения будем считать, что анион соли МAm имеет заряд -1, а активности катиона и аниона равны их концентрациям.
В растворе соли, кроме катиона Мm+ и аниона А-, в пределах координационного числа N образуются комплексные формы: MA(m-1)+, … , MAi(m-i)+, … , MAN(N-m)-.
Константа равновесия комплексной формы MA(m-1)+ равна:
![]() .
.
В общем случае для комплексных форм состава MAi(m-i)+ константа равновесия имеет вид:
![]() .
.
Их называют полными (βi) и ступенчатыми (Ki) константами образования или константами устойчивости.
Суммарная концентрация металла в растворе (СM) равна сумме концентраций всех его форм:
![]() ,
,
Это уравнение называется уравнением материального баланса.
С помощью констант образования bi уравнение материального баланса можно привести к виду:
![]() .
.
Из этого уравнения следует соотношение:
![]() . (3.1)
. (3.1)
Функцию Ф называют функцией Ледена или закомплексованностью.
При описании равновесий комплексообразования часто используют понятие «доля формы aI», которая для комплексных форм определяется выражением:
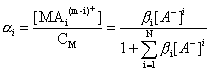 .
.
и изменяется в пределах 0 < aI < 1.
Для катиона Mm+
![]() .
.
В случае большой разницы в ступенчатых константах образования (Ki >> Ki+1) максимальное значение ai может быть практически равным I, a [MAi(m-i)+] » CM. Соответствующую максимуму концентрацию аниона-лиганда можно найти дифференцированием уравнения αi = f([А-]) по концентрации аниона, приравняв производную ![]() нулю.
нулю.
Задача облегчается, если принять, что в материальном балансе дополнительно присутствуют только две соседние формы: MAi-1(m-i+1)+ и MAi+1(m-i-1)+. В результате, получается выражение:
![]() .
.