Изоморфная сокристаллизация является одной из причин соосаждения примесных элементов с осадком соли. Она происходит или в результате истинного изоморфизма, когда микро- и макрокомпонент имеют очень близкие химические и кристалло-химические свойства (например, КСl и RbCl, NiSO4 и CoSO4, RaВr2 и ВaBr2), или благодаря образованию смешанных кристаллов, в которых микро- и макроэлемент находятся в разных степенях окисления.
Для описания распределения микроэлементов между осадком соли и раствором в случае истинного изоморфизма используют:
закон распределения Бертло-Нернста в виде:
![]() ,
,
где Ств и Ср-р – общие концентрации микроэлемента в твердой фазе и в растворе; Kx – константа распределения (константа Хлопина),
или уравнение Гендерсона-Крачека:
![]() , (3.3)
, (3.3)
где а и b – исходные количества микро- и макрокомпонента в растворе; х и у – их количества в твердой фазе; D – коэффициент кристаллизации.
Зависимость между коэффициентом кристаллизации и константой Хлопина описывается соотношением:
![]() ,
,
где С – содержание макрокомпонента в граммах в 1 мл раствора; d – удельный вес твердой фазы.
Однако нужно отметить, что эти уравнения отражают только брутто-распределение микроэлемента и справедливы только для одного состава раствора. При изменении же его состава, например, при добавлении соли с одноименным анионом, как свидетельствуют данные по сокристаллизации RaВr2 с ВaBr2, Kx резко увеличивается. С другой стороны, непонятна связь между Kx и D, которые по определению не зависят от концентрации макрокомпонента.
Подобная ситуация сложилась из-за некорректного применения закона Бертло-Нернста. Если использовать закон распределения в формулировке Нернста, то для распределения радия между осадком BaBr2 и раствором можно написать выражение:
![]() .
.
Поскольку
![]() ,
,
то уравнение приобретает вид:
![]() .
.
В соответствии с этим уравнением постоянство должно наблюдаться для константы K0, а Kx должна быть функцией доли нейтральной формы RаВr2. С другой стороны, согласно следствию из закона Бертло-Нернста постоянство К0 свидетельствует о том, что распределение радия происходит в молекулярной форме RаВr2.
Зависимость между K0 и D описывается уравнением:
![]() , (3.4)
, (3.4)
где x – доля микроэлемента в твердой фазе; р – масса осадка; V – объем раствора.
Поскольку
![]() , а
, а ![]() ,
,
где СМ и ФМ – концентрация и закомплексованность макроэлемента в растворе, то
![]() .
.
Учитывая, что
![]() ,
,
где y – доля макроэлемента в осадке, уравнение (3.4) можно записать следующим образом:
![]() ,
,
где D0 = K0*bm*ПР.
Это уравнение отличается от уравнения Гендерсона-Крачека только тем, что в нем учитываются доли чистых аква-ионов как микро-, так и макроэлемента. При этом очевидно, что коэффициент кристаллизации (D0), и константа распределения (K0) связаны между собой постоянным множителем, не зависящим от концентрации макроэлемента в водном растворе.
Для описания процессов изоморфной сокристаллизации преимущественно используется уравнение Гендерсона-Крачека из-за относительно большего постоянства D (по сравнению с Кx). Это объясняется тем, что при истинном изоморфизме элементы-партнеры очень близки по химическим свойствам (в том числе и по склонности к образованию комплексных форм) и ФМ/Ф » 1. Соответственно
![]() ,
,
в то время как константа Хлопина зависит от склонности к комплексообразованию только микроэлемента.
Учет комплексообразования в системе позволяет выявить закономерности распределения микроэлементов и при сокристаллизации солей разновалентных элементов, образующих, по мнению Хлопина, так называемые аномальные кристаллы, в которых микроэлемент находится в виде микроучастков с собственной кристаллической структурой и имеет нижний концентрационный порог смешиваемости.
Возьмем общий случай, когда микроэлемент ![]() и макроэлемент
и макроэлемент ![]() образуют с анионом An- соединения состава
образуют с анионом An- соединения состава ![]() и
и ![]() . Для упрощения будем считать, что доли полиядерных форм в общем балансе незначительны. Произведя, как и прежде, соответствующие подстановки в уравнении для коэффициента кристаллизации Гендерсона-Крачека (3.3) мы получим следующее выражение:
. Для упрощения будем считать, что доли полиядерных форм в общем балансе незначительны. Произведя, как и прежде, соответствующие подстановки в уравнении для коэффициента кристаллизации Гендерсона-Крачека (3.3) мы получим следующее выражение:
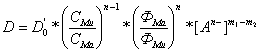 ,
,
где D0’ – постоянная величина; С – общая равновесная концентрация элемента в растворе.
Из-за отсутствия полного объема данных по равновесиям комплексообразования для изученных систем использовать это уравнение довольно затруднительно. Однако на его основе можно сделать следующие выводы:
1) при n > 1 коэффициент кристаллизации (D) будет увеличиваться с ростом концентрации микроэлемента;
2) в случае n = 1 в области малой закомплексованности компонента D будет изменяться пропорционально ![]() .
.