Теория персептронов является основой для изучения многих других типов искусственных нейронных сетей.

В качестве примера простейшей НС рассмотрим трехнейронный персептрон (рис.2.7), то есть такую сеть, нейроны которой имеют активационную функцию в виде единичного скачка*. На n входов поступают некие сигналы, проходящие по синапсам на три нейрона, образующие единственный слой этой НС и выдающие три выходных сигнала:

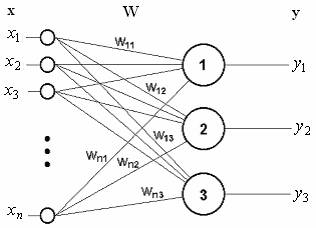
Рис. 2.7. Однослойный персептрон

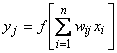, . (2.5)

Очевидно, что все весовые коэффициенты синапсов одного слоя нейронов можно свести в матрицу W, в которой каждый элемент задает величину i-й синаптической связи j-го нейрона. Таким образом, процесс, происходящий в НС, может быть записан в матричной форме:

, (2.6)

где x и y– соответственно входной и выходной сигнальные векторы, f(s) – активационная функция, применяемая поэлементно к компонентам вектора s.

Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера или специализированной микросхемы, на которых обычно реализуется НС. Чем сложнее НС, тем масштабнее задачи, подвластные ей.

Выбор структуры НС осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач уже существуют оптимальные, на сегодняшний день, конфигурации, описанные ниже. Если же задача не может быть сведена ни к одному из известных типов, разработчику приходится решать сложную проблему синтеза новой конфигурации. При этом он руководствуется несколькими основополагающими принципами: возможности сети возрастают с увеличе

* Иногда персептроном называют любую НС слоистой структуры, однако здесь и далее под персептроном понимается только сеть, состоящая из нейронов с активационными функциями единичного скачка (бинарная сеть).

нием числа ячеек сети, плотности связей между ними и числом выделенных слоев.  Введение обратных связей, наряду с увеличением возможностей сети, поднимает вопрос о динамической устойчивости сети; сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов – возбуждающих, тормозящих и др.) также способствует усилению мощи НС. Вопрос о необходимых и достаточных свойствах сети для решения того или иного рода задач представляет собой целое направление нейрокомпьютерной науки. Так как проблема синтеза НС сильно зависит от решаемой задачи, дать общие подробные рекомендации затруднительно. В большинстве случаев оптимальный вариант получается на основе интуитивного подбора.

Сети также можно классифицировать по числу слоев. На рис. 2.8 представлен двухслойный персептрон, полученный из персептрона с рис. 2.7 путем добавления второго слоя, состоящего из двух нейронов. Здесь уместно отметить важную роль нелинейности активационной функции, так как, если бы она не обладала данным свойством или не входила в алгоритм работы каждого нейрона, результат функционирования любой p-слойной НС с весовыми матрицами W⁽ⁱ⁾, i = 1, 2, …, p для каждого слоя i сводился бы к перемножению входного вектора сигналов  на матрицу

W^(S) = W⁽¹⁾ × W⁽²⁾ ×…×W^(p),                                             (2.7)

то есть фактически такая p-слойная НС эквивалентна однослойной НС с весовой матрицей единственного слоя W^(S):

y = W^(S)x.                                                           (2.8)

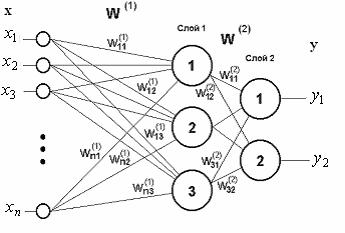
Рис. 2.8. Двухслойный персептрон

Продолжая разговор о нелинейности, можно отметить, что она иногда вводится и в синаптические связи. Большинство известных на сегодняшний день НС используют для нахождения взвешенной суммы входов нейрона формулу (2.1), однако в некоторых приложениях НС полезно ввести другую запись, например:

                                                                (2.9)

или даже

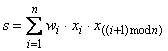.                                       (2.10)

Вопрос в том, чтобы разработчик НС четко понимал, для чего он это делает, какими ценными свойствами он тем самым дополнительно наделяет нейрон и каких лишает. Введение такого рода нелинейности, вообще говоря, увеличивает вычисли

тельную мощь сети, то есть позволяет из меньшего числа нейронов с "нелинейными" синапсами сконструировать НС, выполняющую работу обычной НС с большим числом стандартных нейронов и более сложной конфигурации.

Теперь рассмотрим один нюанс, преднамеренно опущенный ранее. Из рисунка функции единичного скачка видно, что пороговое значение T, в общем случае, может принимать произвольное значение. Более того, оно должно принимать некое произвольное, неизвестное заранее значение, которое подбирается на стадии обучения вместе с весовыми коэффициентами. То же самое относится и к центральной точке сигмоидной зависимости, которая может сдвигаться вправо или влево по оси X, а также и ко всем другим активационным функциям. Это, однако, не отражено в формуле (2.1), которая должна была бы выглядеть так:

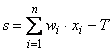.                                                 (2.11)

Дело в том, что такое смещение обычно вводится путем добавления к слою нейронов еще одного входа, возбуждающего дополнительный синапс каждого из нейронов, значение которого всегда равняется 1. Присвоим этому входу номер 0. Тогда

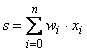,                                                     (2.12)

где w₀ = –T, x₀ = 1.

Очевидно, что различие формул (2.1) и (2.12) состоит лишь в способе нумерации входов.

Из всех активационных функций, изображенных на рис. 2.3, одна выделяется особо. Это гиперболический тангенс, зависимость которого симметрична относительно оси s и лежит в диапазоне [-1,1]. Забегая вперед, скажем, что выбор области возможных значений выходов нейронов во многом зависит от конкретного типа НС.

Какие задачи может решать НС? Работа персептрона сводится к классификации (обобщению) входных сигналов, принадлежащих n-мерному гиперпространству, по некоторому числу классов. С математической точки зрения это происходит путем разбиения гиперпространства гиперплоскостями. Для случая однослойного персептрона:

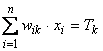, k = 1, …, m.                                       (2.13)

Каждая полученная область является областью определения отдельного класса. Число таких классов для одной НС персептронного типа не превышает 2^m, где m – число выходов сети. Однако не все из них могут быть разделимы данной НС.

Например, однослойный персептрон, состоящий из одного нейрона с двумя входами, представленный на рис. 2.9, не способен разделить плоскость (двумерное гиперпространство) на две полуплоскости так, чтобы осуществить классификацию входных сигналов по классам A и B (табл.2.2).

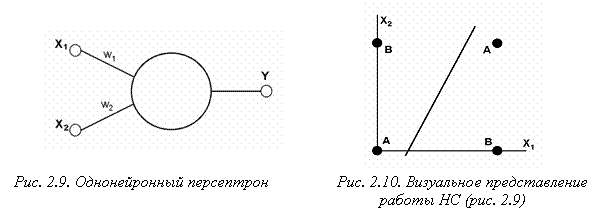
Таблица 2.2 Классификация входных сигналов по классам А и В