Сформулированную в п.3.1 задачу оценивания вне зависимости от топологии НС с позиций нейросетевого подхода можно рассматривать как задачу нахождения неизвестного и реализуемого с использованием нейронной сети отображения ![]() , с помощью которого определяется оценка
, с помощью которого определяется оценка ![]() аналогично выражению (3.2), т.е.:
аналогично выражению (3.2), т.е.:
![]() , (3.4)
, (3.4)
где матрица ![]() определяет массив смещений и весовых коэффициентов НС. В качестве входа НС выступает вектор
определяет массив смещений и весовых коэффициентов НС. В качестве входа НС выступает вектор ![]() , а выходом является вырабатываемая НС оценка
, а выходом является вырабатываемая НС оценка ![]() . В дальнейшем будем рассматривать задачу, в которой
. В дальнейшем будем рассматривать задачу, в которой ![]() , и будем использовать обозначения
, и будем использовать обозначения ![]() ,
, ![]() .
.
Представим выражение (3.3) в виде
![]() .
.
Принимая во внимание это выражение, оценку ![]() будем отыскивать с помощью линейной НС с единственным слоем нейронов, число которых совпадает с размерностью оцениваемого вектора
будем отыскивать с помощью линейной НС с единственным слоем нейронов, число которых совпадает с размерностью оцениваемого вектора ![]() , а их функция активации, зависящая от скалярного аргумента
, а их функция активации, зависящая от скалярного аргумента ![]() , представляет собой тождественное преобразование, т.е.
, представляет собой тождественное преобразование, т.е. ![]() ,
, ![]() . Такую функцию называют также линейной активационной функцией.
. Такую функцию называют также линейной активационной функцией.
Блок-схема, соответствующая такой НС, приведена на рис. 3.1. Здесь для удобства представления введен q-мерный вектор ![]() , совпадающий с
, совпадающий с ![]() , т.е.
, т.е. ![]() ,
, ![]() ; и одинаковый для всех нейронов вход инициализации
; и одинаковый для всех нейронов вход инициализации ![]() . Следует обратить внимание, что количество нейронов совпадает с размерностью вектора состояния
. Следует обратить внимание, что количество нейронов совпадает с размерностью вектора состояния ![]() , а число входов равно общему числу скалярных измерений
, а число входов равно общему числу скалярных измерений ![]() . Обычно
. Обычно ![]() , что и принято при дальнейшем изложении. Скалярные выходы
, что и принято при дальнейшем изложении. Скалярные выходы ![]() сумматоров
сумматоров ![]() определяются как
определяются как ![]() ,
, ![]() . При оценивании скаляра, т.е. при
. При оценивании скаляра, т.е. при ![]() , эта схема вырождается в линейный нейрон, так называемую адалину (adaptive line element-adaline). Поэтому в общем случае при
, эта схема вырождается в линейный нейрон, так называемую адалину (adaptive line element-adaline). Поэтому в общем случае при ![]() ее иногда называют мадалиной.
ее иногда называют мадалиной.
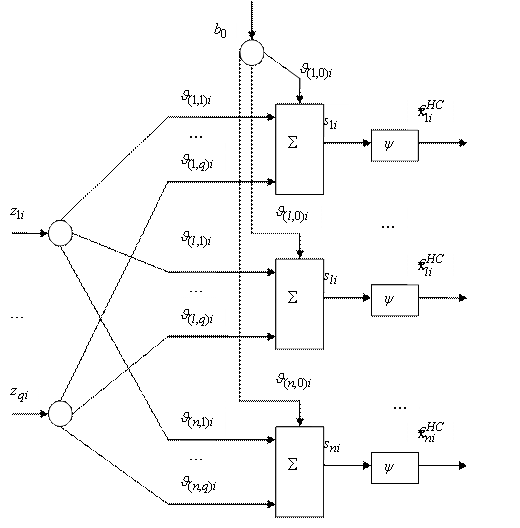
Рис. 3.1. Линейная однослойная НС (мадалина)
С учетом сказанного выражение для оценки, отыскиваемой с помощью нейронной сети, запишем в виде
![]() , (3.5)
, (3.5)
где ![]() –
– ![]() -мерная матрица, включающая
-мерная матрица, включающая ![]() -мерный вектор смещений
-мерный вектор смещений ![]() и
и ![]() -мерную матрицу весовых коэффициентов
-мерную матрицу весовых коэффициентов ![]() , в которой
, в которой ![]() –
–![]() -мерные векторы,
-мерные векторы, ![]() ,
, ![]() .
.
При оценивании случайных последовательностей с помощью НС на основе (3.5) будем полагать, что обучение НС проводится «с учителем», т.е. при использовании набора ![]() , в котором каждый вход
, в котором каждый вход ![]() соответствует истинному значению вектора
соответствует истинному значению вектора ![]() ,
, ![]() , где
, где ![]() – количество пар данных, используемых при обучении. В качестве критерия обучения
– количество пар данных, используемых при обучении. В качестве критерия обучения ![]() выберем функцию вида:
выберем функцию вида:
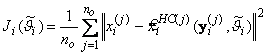 , (3.6)
, (3.6)
где ![]() ;
; ![]() – оценка, вырабатываемая НС по измерениям
– оценка, вырабатываемая НС по измерениям ![]() , соответствующим эталонной реализации
, соответствующим эталонной реализации![]() ;
; ![]() – матрица смещений и весов НС для момента времени
– матрица смещений и весов НС для момента времени ![]() .
.
Интуитивно ясно, что оценка, определяемая с помощью НС вида (3.5), при ее предварительном обучении с использованием критерия (3.6) при увеличении ![]() будет стремиться к оптимальной в среднеквадратическом смысле оценке, задаваемой соотношением (3.3). Показать это достаточно просто. Действительно, предположим, что зафиксирована произвольная совместная плотность распределения
будет стремиться к оптимальной в среднеквадратическом смысле оценке, задаваемой соотношением (3.3). Показать это достаточно просто. Действительно, предположим, что зафиксирована произвольная совместная плотность распределения ![]() для векторов
для векторов ![]() и
и ![]() . Тогда можно записать следующее соотношение:
. Тогда можно записать следующее соотношение:
![]() . (3.7)
. (3.7)
Пределы у многократных интегралов здесь не указываются в целях упрощения записи, но при этом они полагаются, равными ![]() .
.
Если ![]() и
и ![]() для всех
для всех ![]() распределены согласно
распределены согласно ![]() , то, в соответствии с методом Монте-Карло, можно записать:
, то, в соответствии с методом Монте-Карло, можно записать:
 .
.
Таким образом, нейросетевой алгоритм при ![]() фактически строится из условия минимизации критерия вида
фактически строится из условия минимизации критерия вида
![]() ,
,
совпадающего с критерием, используемым при построении оптимального алгоритма. Отсюда следует, что линейный алгоритм (3.5) должен совпадать с алгоритмом, оптимальным в классе линейных. Покажем это путем непосредственного доказательства.
Используя (3.5), критерий (3.6) представим в виде
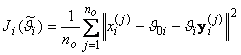 . (3.8)
. (3.8)
Найдем значения ![]() и
и ![]() , минимизирующие это выражение. Продифференцируем (3.8) по
, минимизирующие это выражение. Продифференцируем (3.8) по ![]() ,
, ![]() и приравняем производные нулю:
и приравняем производные нулю:
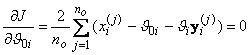 ;
;
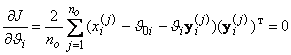 .
.
После несложных преобразований можем записать:
![]() ; (3.9)
; (3.9)
![]() , (3.10)
, (3.10)
где
![]() ;
; ![]() , (3.11)
, (3.11)
![]() ;
; ![]() .
.
Подставив (3.9) в (3.10), получим:
![]() .
.
или
![]() , (3.12)
, (3.12)
где
![]() ; (3.13)
; (3.13)
![]() . (3.14)
. (3.14)
Таким образом, в результате обучения НС (3.5) в соответствии с критерием (3.6) вектор смещений ![]() будет задаваться выражением (3.6), а матрица весовых коэффициентов
будет задаваться выражением (3.6), а матрица весовых коэффициентов ![]() выражением (3.12), которое при невырожденности
выражением (3.12), которое при невырожденности ![]() может быть записано как:
может быть записано как:
![]() . (3.15)
. (3.15)
Отсюда следует, что оценка ![]() , получаемая по измерениям
, получаемая по измерениям ![]() с помощью НС (3.5), обученной согласно критерию (3.6), может быть представлена в виде:
с помощью НС (3.5), обученной согласно критерию (3.6), может быть представлена в виде:
![]() , (3.16)
, (3.16)
где ![]() ;
; ![]() ;
; ![]() ,
, ![]() определяются уравнениями (3.11), (3.13), (3.14) и представляют собой выборочные значения математических ожиданий и соответствующих матриц ковариаций.
определяются уравнениями (3.11), (3.13), (3.14) и представляют собой выборочные значения математических ожиданий и соответствующих матриц ковариаций.
Выражения (3.16) и (3.3) совпадают по форме, что говорит о том, что НС (3.5) при соответствующем обучении в условиях, когда указанные выборочные значения близки к своим истинным значениям, обеспечивает нахождение оценки, близкой к оптимальной.
Полученный результат позволяет трактовать оптимальный в линейном классе алгоритм как нейронную сеть простейшего вида, обучаемую в соответствии с критерием (3.6).
С практической точки зрения этот результат может быть полезным в тех ситуациях, когда имеются большие массивы исходных данных, которые могут быть привлечены для обучения сети. В этом случае можно построить процедуру оценивания, не проводя предварительной идентификации свойств оцениваемых последовательностей.
При построении используемых в прикладных задачах алгоритмов оценивания важным представляется умение находить не только саму оценку, но и соответствующую ей расчетную характеристику точности. В качестве такой характеристики точности для оптимальной в среднеквадратическом смысле оценки может быть использована апостериорная матрица ковариаций ошибок вычисляемая с помощью следующего соотношения:
![]() . (3.17)
. (3.17)
Хотя при построении нейросетевого алгоритма не предполагалась выработка какой-либо характеристики точности оценивания, аналогичной матрице ковариаций
(3.17), ясно, что такая характеристика после обучения НС в принципе может быть рассчитана как
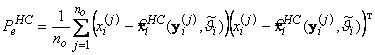 . (3.18)
. (3.18)
Аналогично решается задача и для сглаживания ![]() , и для прогноза
, и для прогноза ![]() .
.