Проиллюстрируем полученный результат на простейшем примере.

Пусть необходимо оценить значения экспоненциально-коррелированного процесса

,                                       (3.19)

используя измерения

,                      ,                               (3.20)

проведенные в дискретные моменты времени  с интервалом .

В уравнении (3.19):  – дисперсия процесса;  – интервал корреляции; – центрированный гауссовский белый шум единичной интенсивности. Предполагается, что значение процесса  в начальный момент времени представляет собой независимую от  центрированную гауссовскую случайную величину с нулевым математическим ожиданием и дисперсией . Ошибки измерения  в (3.20) считаются независимыми между собой и от  гауссовскими случайными величинами с дисперсией .

В разностном виде уравнение (3.19) записывается как

,                                (3.21)

где  – независимые между собой и от  и  центрированные гауссовские случайные величины с дисперсией .

Для нахождения оптимальной оценки реализуется нерекуррентный алгоритм в соответствии с (3.3) при . Для сопоставления этого алгоритма с НС используется расчетная матрица ковариаций, вычисляемая согласно (3.18).

Для нейросетевого алгоритма оценивания выбрана однослойная НС, соответствующая схеме, представленной на рис. 3.1, с одним слоем, содержащим один нейрон (по числу оцениваемых переменных), и тождественной функцией активации (рис.3.2).

При обучении НС моделировались реализации , , , в соответствии с (3.20) и (3.21) Общее число реализаций , . Далее с их использованием осуществлялось обучение согласно критерию (3.6) на основе правила Уидроу-Хоффа. После обучения проводилось проверка. С этой целью дополнительно моделировалось еще 300 пар реализаций последовательностей (3.21) и (3.20) длиной .

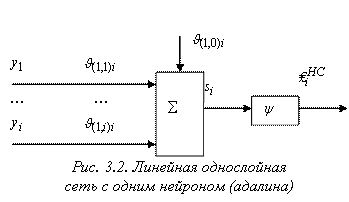
При моделировании были выбраны следующие параметры: ; ; ; .

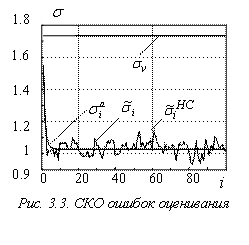
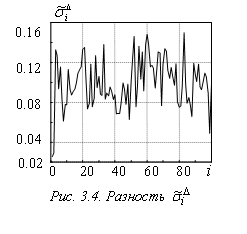
На рис. 3.3, 3.4 представлены:

·  расчетное среднее квадратическое отклонение (СКО) ошибок оценивания, вычисляемое с использованием (3.17);

·  выборочные действительные СКО ошибок оценивания  и  для оптимального и нейросетевого алгоритмов, вычисляемые как

;           ,

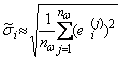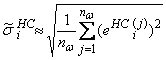где  ;           ;

·  СКО разности выходов  оптимального и нейросетевого алгоритмов, определяемое как

.

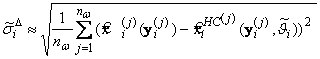Ясно, что в данном случае  по смыслу совпадает с , задаваемой выражением (3.18).

В этих соотношениях принималось: , , .

Как видно из рис. 3.3, 3.4, оценка обученной НС практически совпадет с оптимальной оценкой, а значения   почти на порядок меньше СКО ошибок  и .