Алгебраическое произведение A и B обозначается A×B и определяется так:
"xÎE mA×B (x) = mA(x)mB(x).
Алгебраическая сумма этих множеств обозначается ![]() и определяется так:
и определяется так:
"xÎE ![]() = mA(x) + mB(x) — mA(x)mB(x).
= mA(x) + mB(x) — mA(x)mB(x).
Для операций {×, ![]() } выполняются свойства:
} выполняются свойства:
· 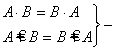 коммутативность;
коммутативность;
· 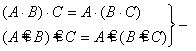 ассоциативность;
ассоциативность;
· A×Æ = Æ, A![]() Æ = A,
Æ = A, ![]() = A, A
= A, A![]() E = E;
E = E;
· 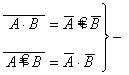 теоремы де Моргана.
теоремы де Моргана.
Не выполняются:
· 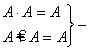 идемпотентность;
идемпотентность;
· 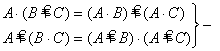 дистрибутивность;
дистрибутивность;
· ![]() = Æ, A
= Æ, A![]()
![]() = E.
= E.
Замечание. При совместном использовании операций {È, Ç, +, ×} выполняются свойства:
· А×(BÈC) = (A×B)È(A×C);
· А×(BÇC) = (A×B)Ç(A×C);
· А![]() (BÈC) = (A
(BÈC) = (A![]() B)È(A
B)È(A![]() C);
C);
· А![]() (BÇC) = (A
(BÇC) = (A![]() B)Ç(A
B)Ç(A![]() C).
C).
На основе операции алгебраического произведения (по крайней мере, для целых ![]() эта основа очевидна) определяется операция возведения в степень
эта основа очевидна) определяется операция возведения в степень ![]() нечеткого множества A, где
нечеткого множества A, где ![]() – положительное число. Нечеткое множество
– положительное число. Нечеткое множество ![]() определяется функцией принадлежности
определяется функцией принадлежности ![]() Частным случаем возведения в степень являются:
Частным случаем возведения в степень являются:
· CON(A) = A2 – операция концентрирования,
· DIL(A) = A0,5 – операция растяжения,
которые используются при работе с лингвистическими неопределенностями (рис. 4.4).
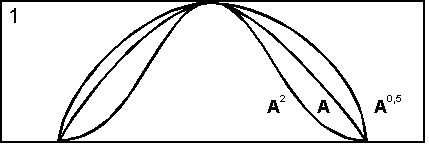
Рис. 4.4. Иллюстрация к понятию операций
концентрирования (уплотнения) и растяжения
Умножение на число. Если ![]() – положительное число, такое, что
– положительное число, такое, что ![]() , то нечеткое множество aA имеет функцию принадлежности:
, то нечеткое множество aA имеет функцию принадлежности:
maA(x) = amA(x).
Выпуклая комбинация нечетких множеств. Пусть A1, A2,…, An – нечеткие множества универсального множества E, а w1, w2, …, wn – неотрицательные числа, сумма которых равна 1. Выпуклой комбинацией A1, A2,…, An называется нечеткое множество A с функцией принадлежности:
"xÎE mA(x1, x1,…, xn) = w1mA1(x) + w2mA2(x) + … + wnmAi(x).
Декартово произведение нечетких множеств. Пусть A1, A2,.., An – нечеткие подмножества универсальных множеств E1, E2,…, En соответственно. Декартово произведение A = A1 ´ A2 ´ …´ An является нечетким подмножеством множества E = E1´E2´…´En с функцией принадлежности:
mA(x1, x2, …, xn) = min{ mA1(x1), mA2(x2) , … , mAi(xn)}.
Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества.
Пусть A – нечеткое множество, E – универсальное множество и для всех xÎE определены нечеткие множества K(х). Совокупность всех K(х) называется ядром оператора увеличения нечеткости ![]() . Результатом действия оператора
. Результатом действия оператора ![]() на нечеткое множество A является нечеткое множество вида:
на нечеткое множество A является нечеткое множество вида:
![]() (A, K) =
(A, K) = ![]() mA(x)K(х),
mA(x)K(х),
где mA(x)K(х) – произведение числа на нечеткое множество.
Пример:
E = {1,2,3,4}; A = 0,8/1 + 0,6/2 + 0/3 + 0/4; K(1) = 1/1 + 0,4/2; K(2) = 1/2 + 0,4/1 + 0,4/3;
K(3) = 1/3 + 0,5/4; K(4) = 1/4.
Тогда
H(A,K) = mA(1) K(1) È mA(2)K(2) È mA(3)K(3) È mA(4)K(4) =
= 0,8(1/1 + 0,4/2) È 0,6(1/2 + 0,4/1 + 0,4/3) = 0,8/1 + 0,6/2 + 0,24/3.
Четкое множество a-уровня (или уровня a). Множеством a-уровня нечеткого множества A универсального множества E называется четкое подмножество Aa универсального множества E, определяемое в виде:
Aa = {x/mA(x)³a}, где a £ 1.
Пример: A = 0,2/x1 + 0/x2 + 0,5/x3 + 1/x4.
Тогда A0.3 = {x3, x4}, A0.7 = {x4}.
Свойство множества a-уровня: если a1 ³ a2, то Aa1 £ Aa2.