Опишем типовой подход к построению алгоритмов обучения и использования нечетких нейронных сетей. Предположим, что нечеткой нейронной сетью должно быть реализовано (неизвестное) отображение:

 

при наличии обучающего множества:

.

Для моделирования неизвестного отображенияиспользуем упрощенный алгоритм нечеткого вывода, применяя следующую форму записи предикатных правил:

: если  есть , и , есть  и … и , есть , то    

где  — нечеткие числа треугольной формы,  — вещественные числа.

Степень истинности i-го правила определяется с помощью операции умножения (Larsen):

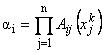
(можно использовать и другие представления для моделирования логического оператора «И»).

Выход нечеткой системы определяется в соответствии с центроидным методом (дискретный вариант):

.

Введение функции ошибки для k-го предъявленного образца вида:

позволяет далее, как в обычных нейронных сетях, использовать градиентный метод для подстройки параметров заданных предикатных правил. Так, величины z_i можно корректировать по соотношению:

где - константа, характеризующая скорость обучения.

Для того чтобы проиллюстрировать идею построения структуры нечеткой нейронной сети, рассмотрим пример нечеткой системы, имеющей следующую базу знаний:

;

;                  (5.1)

,  

где ,  и – входные переменные; – выход системы; , , ,, , , , , – некоторые нечеткие множества с функциями принадлежности заданного типа

(например, сигмоидного типа), которые зависят в общем случае от вектора параметров :

 ;

     

.

Для определения выходной переменной используем алгоритм вывода Tsukamoto, в соответствии с которым:

·  подсчитываются значения истинности предпосылок для каждого правила:

;                                                       

;                                                    

,                                                   

где , , – текущие значения входов системы;

·  для каждого правила определяются частные выходы:

;

;

;

·  находится общий выход системы:

.

Изложенный процесс иллюстрируется рис. 5.2.

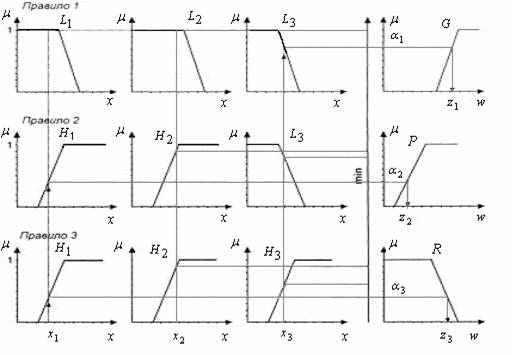
Рис.5.2. Иллюстрация алгоритма вывода в нечеткой нейронной сети

Нечеткая НС, реализующая приведенный механизм вывода, представлена на рис.5.3.

Заметим, что сети с подобной архитектурой в англоязычной литературе получили название ANFIS (Adaptive Neuro-Fuzzy Inference System).

Данная сеть может быть описана следующим образом.

Слой 1. Выходы нейронов этого слоя представляют собой значения функций принадлежности при конкретных (заданных) значениях входов.

Слой 2. Выходами нейронов этого слоя являются степени истинности предпосылок каждого правила базы знаний системы, вычисляемые по формулам

;                                                       

;                                                    

.                                                   

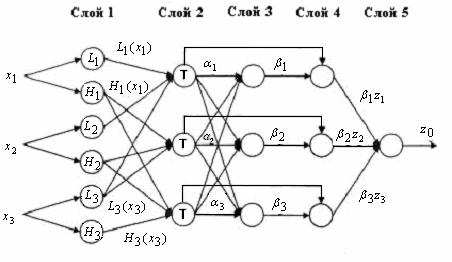Рис. 5.3. Структура нечеткой нейронной системы (архитектура ANFIS)

Все нейроны слоя обозначены буквой , что означает, что они могут реализовывать произвольную -норму для моделирования операции «И».

Слой 3. Нейроны этого слоя вычисляют величины:

;    ;   .

Слой 4. Нейроны данного слоя выполняют операции:

;     ;   .

Слой 5. Единственный нейрон этого слоя вычисляет выход сети:

.

Корректировка параметров системы для функций принадлежности G, P и R производится в соответствии с ранее рассмотренным подходом. Так, например, настройка коэффициентов для функций принадлежности , и  осуществляется по формулам

;

;

где

Соответствующие выражения могут быть получены и для остальных коэффициентов: b_i и с_i, i = 1, 2, 3.