В исследованиях экономических объектов и явлений метод математического моделирования находится в начале своего пути, однако с помощью этого метода уже получены многие серьезные результаты. Ряд математических моделей нашел широкое практическое применение в экономике. К таким моделям относятся: задача линейного программирования, транспортная задача, задачи сетевого планирования, линейные балансовые модели и их обобщения, некоторые модели динамического программирования и т.д. Некоторые модели имеют теоретический интерес, т.к. они помогают раскрыть смысл или дать интерпретацию понятий экономики на математическом языке.
По степени сложности математические модели экономических объектов и явлений могут быть с известной степенью условности подразделены на несколько основных типов (см. рис. 1.1).
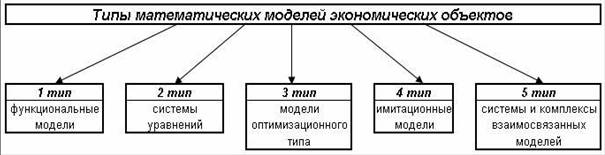
Рис. 1.1
К первому типу относятся функциональные модели, которые выражают, как правило, прямые зависимости между известными (экзогенными) и неизвестными (эндогенными) величинами. Необходимые для построения модели параметры определяются на основе нормативных данных или статистическими способами.
Модели второго типа – это модели, выраженные с помощью систем уравнений относительно эндогенных величин. Они выражают обычно балансовые соотношения между различными экономическими показателями и используются для нахождения сбалансированных плановых решений (например, модель межотраслевого баланса). С математической точки зрения, проблема соответствующей математической задачи не представляет принципиальной трудности, однако в случае большого количества уравнений и неизвестных требует использования ЭВМ с высоким быстродействием и большой памятью.
Третья группа – модели оптимизационного типа, т.е. такие модели, в которых имеется какая-либо целевая функция, которая измеряет качество принимаемого решения. Основную часть такой модели составляет также система уравнений или неравенств относительно эндогенных величин. При этом необходимо найти такое решение этой системы, которое давало бы оптимальное (т.е. максимальное или минимальное в зависимости от постановки конкретной задачи) значение некоторого экономического показателя. Основными моделями этого типа, применяемыми в планировании, являются задачи линейного программирования. С математической точки зрения, построение оптимизационных моделей представляет трудную и еще до конца не разработанную проблему.
К четвертой группе математических моделей относятся так называемые имитационные модели, которые используются обычно в составе человеко-машинных или игровых имитационных систем.
Имитационные модели характеризуются, прежде всего, весьма точным отображением экономического процесса или явления, в связи с чем получаемые математические задачи оказываются довольно сложными, в них присутствуют нелинейные и стохастические (вероятностные) зависимости и переменные. Основной способ решения подобных задач лежит на пути использования специальным образом упорядоченных вариантных расчетов на ЭВМ и, что очень важно, привлечения специалистов к решению задачи оптимального выбора.
Пятую группу составляют более сложные образования, такие, как системы и комплексы взаимосвязанных моделей, относящихся к перечисленным выше типам. Развитие систем моделей позволяет точнее отразить самые различные аспекты планирования и функционирования экономических объектов, в частности находить оптимальные решения, сочетающие рациональное соотношение между отраслевым и территориальным аспектами планирования и управления. Проблема нахождения согласованного решения в системе моделей является серьезной математической задачей, которая должна быть решена в плане создания необходимых методов и в плане разработки программного обеспечения для ЭВМ.
Указанные выше функциональные модели используются для предплановых расчетов определения потребности в сырье, материалах, полуфабрикатах на промышленных предприятиях. Модели того же типа, основанные на экономических моделях статистических данных, используются для углубленного анализа процессов социально-экономического развития. С их помощью осуществляется надежное прогнозирование основных показателей производства, потребления, демографические прогнозы, а также прогнозы развития науки, техники и окружающей среды.
Широкое применение находят в работе плановых органов математические модели, выраженные с помощью систем уравнений, в особенности модели межотраслевого баланса (МОБ). Эти модели постоянно используются для определения сбалансированных планов производства и распределения готовой продукции, а также расчета капитальных вложений и материального производства. Модели подобного типа применяются и для формирования планов предприятий, а также для решения ряда экологических задач.
Большую экономию транспортных средств и горючего дает решение задач на минимум транспортных затрат в области транспортных перевозок. Разработаны и реализованы в ряде отраслей модели оптимизации развития и размещения производства и транспортировки продукции по критерию минимума приведенных или, в динамической постановке, интегральных затрат. Планы размещения производства, основанные на решении этих задач, позволяют получить экономию до 5-7 % капитальных вложений и снижение себестоимости продукции на 2-5 % по сравнению с планами, составленными обычными методами, без применения математических моделей. Применение оптимизационных моделей для решения проблем рационализации структуры производства и путей использования продукции ряда отраслей дает возможность снизить приблизительно на 8-12 % плановые объемы капитальных вложений и на 5-7 % плановые величины эксплуатационных затрат.
В настоящее время усиленно разрабатываются и предлагаются для использования в плановых органах и хозяйственных организациях человеко-машинные имитационные системы, которые позволяют сочетать в режиме диалога «человек – ЭВМ» знание и опыт практических работников с формальными процедурами принятия решения.
Развитие вычислительной техники сделало возможным проведение больших объемов вычислений за сравнительно короткое время. Это обстоятельство позволило перейти к разработке более точных моделей реальных объектов, в которых учитываются нелинейные и стохастические связи, применять методы имитационного моделирования,
основанные на большом числе повторных расчетов и последующей статистической обработке, а также решать оптимизационные задачи большой размерности с удовлетворительной точностью. Важной особенностью развития вычислительной техники является развитие периферийных устройств, операционных систем и средств взаимодействия человека-эксперта с ЭВМ в диалоговом режиме. Последнее обстоятельство позволило перейти к решению слабо структурированных задач во многих областях науки и техники с помощью способов, основанных на сочетании формальных и неформальных (с участием человека-эксперта) методов.
Потребность в решении таких задач связана с естественным расширением круга исследований – от решения хотя и сложных, но все же изолированных проблем к изучению проблем, имеющих по существу комплексный характер. Последнее означает, что появляется необходимость рассматривать возникающие задачи в целостном образе, не разрушая и не подменяя существующие взаимосвязи внутри сложной системы. Всякое более или менее точное описание условий подобной задачи, как правило, приводит к проблеме выбора наилучшего (оптимального, рационального) решения в условиях неопределенности и необходимости сделать выбор по многим критериям.
Существующие формальные методы решения подобных задач обычно приводят к множественности достаточно равноценных ответов, а для практических целей необходимо выбрать только один (или очень малое количество) вариант решения. Использование опыта и знаний экспертов позволяет во многих случаях удовлетворить это требование. При этом работа в диалоговом режиме дает возможность осуществить целенаправленный выбор за достаточно малое время. Применение диалоговых методов позволяет построить эффективный инструмент для решения целых серий сложных задач, которые относятся к определенному типу реальных объектов.
При исследовании экономических задач диалоговые системы выступают как инструмент для совместного (эксперт и ЭВМ) решения этих задач, характеризующийся следующими чертами:
ü возможность организации вычислительного процесса таким образом, чтобы эксперт оказывал воздействие на ход решения в фиксированные моменты расчета (точки ветвления);
ü существование в самой вычислительной системе возможности получать необходимую информацию от эксперта, в том числе некоторые элементы обучения эксперта (лица принимающего решения – ЛПР, пользователя);
ü возможность учета неформальных (или трудноформализуемых) факторов, которые являются существенными в определенной экономической обстановке;
ü возможность использования специальных эвристических методов для решения сложных математических задач, связанных с экономическими моделями;
ü возможность определять с помощью эксперта наиболее подходящие решения многокритериальных оптимизационных задач, отражающих различия интересов участников экономического процесса;
ü возможность исследовать на модельном уровне последствия предлагаемых управленческих и хозяйственных решений.
Возможность исследования последствий принимаемых решений с помощью диалоговой системы является одним из главнейших ее достоинств. Важно также то, что в качестве экспертов могут работать специалисты, хорошо понимающие интересы тех или иных участников экономического процесса. Участие такого рода экспертов позволяет получать согласованные решения в сложных комплексных системах, где интересы участников либо не полностью совпадают, либо противоречат друг другу.
Многие исследования сложных экономических объектов имеют комплексный характер, поскольку в этих работах, как правило, объединены вопросы анализа произ
водства, его ресурсного обеспечения, распределения, потребления, повышения уровня жизни, его воздействия на трудовую активность населения и т.д. В этих работах принимают участие специалисты по экономико-математическому моделированию, по проблемам совершенствования хозяйственного механизма, социально-экономической эффективности и др.
Разработка диалоговых систем позволяет объединить усилия указанных групп специалистов для исследования сложных комплексных процессов. При этом специалисты чисто экономического профиля участвуют в работе диалоговых систем в качестве экспертов, оценивающих результаты работы системы. Специалисты по экономико-математическому моделированию занимаются вопросами совершенствования «начинки» диалоговой системы – ее модельной основы. Специалисты по программному обеспечению и вычислительной технике работают над совершенствованием программных и вычислительных средств, обеспечивающих эффективную работу диалоговой системы.