Аналитическая модель операционного анализа является дальнейшим развитием статистической модели. Основное ее отличие от статистической модели состоит в том, что для ее реализации не требуется знать значения базисных переменных, получаемых в результате наблюдений за исследуемой системой в априори установленном интервале времени. Поэтому она может быть использована и на предварительных этапах проектирования создаваемых производственных систем для технико-экономического обоснования принимаемых проектных решений и когда исследуются различного рода экономические и социальные процессы.
В данной главе дается изложение алгоритма аналитической модели операционного анализа и на ее основе производится синтез проектируемых систем, удовлетворяющих следующим критериям:
Ø достижение максимума суммарной стоимости мощностей всех модулей ПС при условии, что продолжительность нахождения каждой выполняемой в ПС работы ограничена сверху (
);
Ø обслуживание в ПС многомерного потока работ, имеющих в общем случае различные приоритеты в очередности их приема на выполнение.
На базе построенной аналитической модели операционного анализа создается метод по управлению инвестиционным процессом в проектируемых коммерческих процессах (системах).
Для реализации предлагаемой аналитической модели необходимо иметь следующие виды исходной информации:
— количество работ 
, которые выполняются в проектируемой системе за плановое время 
;
— вектор технологии выполнения работы 
в проектируемой системе, устанавливающий очередность использования модулей (подсистем) ПС в процессе выполнения ;
— средняя величина резервирования мощности j-го (
) модуля 
проектируемой ПС;
— трудоемкость выполнения работы модулем при разовом обращении к нему ;
— вектор, определяющий величины дефицитных ресурсов, включая и финансовые, необходимых для выполнения в ПС;
— интенсивность поступления в ПС ресурсов 
-го 
вида, необходимых для выполнения работ .
Рассмотрим форму задания каждого из указанных видов исходной информации.
При задании компонентов вектора учитывается, что в процессе выполнения работы каждая подсистема ПС может быть использована многократно. С учетом указанного вектор представляется в виде
,
где 
— порядковый номер подсистемы ПС, используемой при выполнении работы в 
-ю очередь.
Значение коэффициента резервирования 
определяет долю мощности модуля 
, которая резервируется для решения в перспективе конкретных задач, например, для увеличения производительности ПС в целом.
Трудоемкость 
есть количество операций, исполняемых модулем проектируемой ПС при разовом выполнении им работы 
.
На практике для определения точечного значения трудоемкости поступают следующим образом:
ü определяют 
— среднее время выполнения работы 
модулем , мощность (быстродействие) которого 
известна по многократному использованию в ретроспективе;
ü считают, что
. (4.18)
Справедливость формулы (4.18) следует из очевидного факта, что быстродействие модуля не влияет на трудоемкость выполняемой им работы .
Параметры , , 
, а также компоненты вектора 
задаются в табл. 4.1.
Таблица 4.1
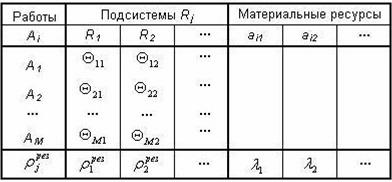
Значения исходных параметров (см. табл. 4.1) являются нормативными. Они получены с помощью соответствующих экспериментов, стандартов, корреляционных зависимостей, уравнений регрессии, экстраполяции трендов и т.д.
Алгоритм данной модели (метода аналитического моделирования процесса выполнения работ в ПС) состоит в выполнении следующей последовательности операций:
1. Определение производительности ПС в целом (
).
2. Нахождение значений коэффициентов 
и 
, где 
есть число переходов работы при ее выполнении в ПС от модуля к модулю 
, а
; 
; 
.
3. Определение производительности каждого модуля ПС 
.
4. Вычисление средней трудоемкости выполнения модулем одной работы 
.
5. Установление нижнего предела мощности 
-го 
модуля ПС (
).
Рассмотрим в отдельности каждую из указанных операций.
1. Величина 
в зависимости от сложившихся конкретных условий может быть определена одним из следующих способов:
ü исходя только из наличия материальных ресурсов (см. табл. 4.1);
ü по формуле 
, исходя только из количества заданных работ 
, и планового времени 
, за которое они должны быть выполнены в ПС;
ü на основе рыночных цен на производственные и материально-технические ресурсы, используемые при создании ПС.
2. Коэффициенты 
и 
находятся через векторы технологии 
. Предположим, например, что 
. В этом случае имеем:
ü 
а все остальные значения 
;
ü 
;
ü 
.
3. Производительность каждого -го модуля ПС 
, , находится так же, как и в статистической модели операционного анализа, по формуле
.
Однако в данной модели для определения значений 
может быть использован и другой метод, а именно решение системы уравнений баланса:
, (4.19)
где 
— частота перехода от подсистемы (модуля) 
к подсистеме , определяемая по формуле
. (4.20)
Система уравнений (4.19) имеет единственное нетривиальное решение относительно , , только при заданном значении 
— производительности ПС в целом.
4. Значение трудоемкости 
находится по формуле
, (4.21)
где 
— трудоемкость выполнения работы 
модулем , а отношение 
есть вероятность того, что модуль выполняет работу .
5. Последней, завершающей операцией по разработке алгоритма аналитической модели процесса выполнения заданных работ в многомодульной системе ПС является установление нижнего предела мощности (быстродействия) каждого модуля .
Ввиду того, что коэффициент загрузки 
модуля 
должен удовлетворять условию
,
имеем
или
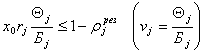. (4.22)
Из формулы (4.22) следует, что
.
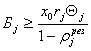Используя формулу (4.21), окончательно находим
. (4.23)
В тех случаях, когда производительность ПС 
, а 
(
— максимально допустимая величина загрузки ), формула (4.23) приводится к виду
. (4.24)
Зная конкретные значения мощностей модулей ПС 
, удовлетворяющих условиям (4.23) и (4.24), можно определить все основные показатели функционирования ПС.
Многокритериальный метод синтеза проектируемых систем
На практике достаточно часто при формировании проектируемых структур выдвигается требование, чтобы кроме выполнения условия (4.24) среднее время выполнения заказа, пребывания каждой работы 
в проектируемой системе, не превышало бы заданного предела 
, т.е. выполнялось бы условие
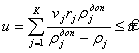. (4.25)
Решение указанной двухкритериальной задачи синтеза ПС выполняется в следующей последовательности:
ü по методу, изложенному выше в этом же разделе. Находятся значения мощности 
, модулей ПС;
ü устанавливается рыночная цена 
, каждого модуля 
ПС в соответствии с его мощностью;
ü определяется общая стоимость всех 
модулей проектируемой ПС
;
ü если выполняется условие (4.25), то считается, что мощность модулей ПС является оптимальной. Если это условие не выполняется, то определяются новые значения мощностей ПС.
Для нахождения оптимальных значений мощности ПС 
, удовлетворяющих условию (4.25), используется метод множителей Лагранжа. При этом предполагается, что стоимость 
каждого модуля 
, прямо пропорциональна его мощности, т.е.
.
Данная задача решается методом множителей Лагранжа при следующей постановке: требуется определить такие значения мощности модулей ПС , при которых суммарная стоимость всех ее модулей
достигает минимума при условии, что среднее время выполнения (нахождения) в ПС одной работы не превосходит 
, т.е. 
.
Для решения поставленной задачи строится целевая функция
,
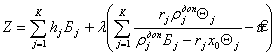где
— неопределенный множитель Лагранжа.
Находятся частные производные от 
по неизвестным параметрам :
.
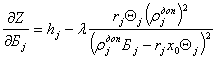Строится система нормальных уравнений:
,
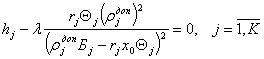и находится ее решение:
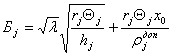. (4.26)
Для определения значения множителя Лагранжа используется равенство (4.26) и указанное выше условие 
:
. (4.27)
Подставив выражение для 
, определяемое по формуле (4.27), в формулу (4.26), находим конечные формулы для определения оптимальных значений мощности ПС , и минимальной совокупной стоимости мощности всех модулей ПС 
, удовлетворяющих критериям 
и :
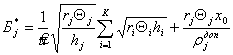; (4.28)
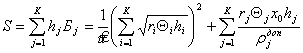. (4.29)
По аналогии с изложенным методом синтеза ПС по двум критериям можно построить и метод синтеза ПС по трем и большему числу критериев. Например, можно
выполнить синтез ПС по двум рассмотренным критериям (
и 
) и по третьему критерию (
), означающему, что средняя продолжительность пребывания в очереди у модуля 
для каждой выполняемой в ПС работы не должна превышать 
-й части продолжительности ее обслуживания этим модулем ПС.