Человеческое мышление устроено так, что мир представляется состоящим из отдельных «объектов». Философам давно известно, что мир – единое неразрывное целое, и выделение в нем объектов – это не более чем произвольный акт нашего мышления, позволяющий сформировать доступную для рационального анализа картину. Но как бы то ни было, выделение объектов и их совокупностей – естественный способ организации нашего мышления, поэтому не удивительно, что он лежит в основе главного инструмента описания точного знания – математики.

Понятие множества принадлежит к числу фундаментальных неопределяемых понятий математики. О множестве известно как минимум, что оно состоит из элементов. Для определенности примем следующие формулировки.

Определение. Под множеством S будем понимать любое собрание определенных и различимых между собой объектов, мыслимое как единое целое. Эти объекты называются элементами множества S.

Определение. Под множеством понимают объединение в единое целое определенных вполне различаемых предметов (объектов), которые при этом называются элементами образуемого ими множества.

Обычно множества обозначают прописными буквами латинского алфавита: A, B, C, …; а элементы множеств – строчными буквами: a, b, c, … .

Если объект х является элементом множества М, то говорят, что х принадлежит М: хМ. В противном случае говорят, что х не принадлежит М: хМ.

В этом интуитивном определении, принадлежащем немецкому математику     Г. Кантору, существенным является то обстоятельство, что собрание предметов само рассматривается как один предмет, мыслится как единое целое. Что касается самих предметов, которые могут входить в множество, то относительно них существует значительная свобода.

Пример 1

Это может быть множество студентов, обучающихся в университете, множество простых чисел и т. д.

Определение. Множество А называется подмножеством множества В, если всякий элемент из А является элементом В (обозначают). Если А является подмножеством В и В не является подмножеством А, то говорят, что А является строгим (собственным) подмножеством В (обозначают ).

Определение. Множество, не содержащее элементов, называется пустым (обозначают Æ), оно является подмножеством любого множества. Множество U называется универсальным, то есть все рассматриваемые множества являются его подмножеством.

Рассмотрим два определения равенства множеств.

Определение. Множества А и В считаются равными, если они состоят из одних и тех же элементов, пишут А=В, в противном случае А¹В.

Определение. Множества А и В считаются равными, если

Существуют следующие способы задания множеств:

1) перечислением элементов: М = {a₁, a₂, …, a_k}, т. е. списком своих элементов;

2) характеристическим предикатом: М = {x | P(x)} (описанием характеристических свойств, которыми должны обладать его элементы);

порождающей процедурой: M = { x | x=f}, которая описывает способ получения элементов множества из уже полученных элементов либо других объектов. В таком случае элементами множества являются все объекты, которые могут быть

1) построены с помощью такой процедуры. Например, множество всех целых чисел, являющихся степенями двойки.

Замечание. При задании множеств перечислением обозначения элементов обычно заключают в фигурные скобки и разделяют запятыми. Перечислением можно задавать только конечные множества (число элементов множества конечно, в противном случае множество называется бесконечным). Характеристический предикат – это некоторое условие, выраженное в форме логического утверждения или процедуры, возвращающей логическое значение. Если для данного элемента условие выполнено, то он принадлежит определяемому множеству, в противном случае – не принадлежит. Порождающая процедура – это процедура, которая, будучи запущенной, порождает некоторые объекты, являющиеся элементами определяемого множества. Бесконечные множества задаются характеристическим предикатом или порождающей процедурой.

Пример 2

1) М = {1, 2, 3, 4} – перечисление элементов множества.

2)  — характеристический предикат.

Определение. Мощность конечного множества А – это число его элементов.

Мощность множества обозначают: |A|.

Пример 3

|| = 0; |{}| = 1.

Определение. Множества называются равномощными, если их мощности совпадают.

Определение. Множество всех подмножеств множества А называется булеаном P(A).

Известно, что если множество А содержит n элементов, то множество P(A) содержит 2ⁿ элементов. В связи с этим используется также обозначение множества-степени множества А в виде 2^А.

Пример 4

А = {0, 1, 2}, P(A) = { , {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}}.

Геометрически множества можно представить с помощью диаграмм Эйлера-Венна. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Операции над множествами рассматриваются для получения новых множеств из уже существующих.

Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1.1):

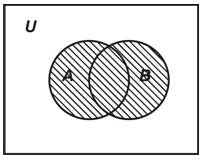
Рис. 1.1. Диаграмма Эйлера-Венна для объединения

Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 1.2):

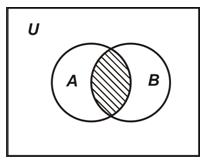
Рис. 1.2. Диаграмма Эйлера-Венна для пересечения

Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 1.3):

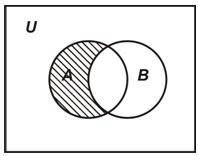
Рис. 1.3. Диаграмма Эйлера-Венна для разности

Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 1.4):

Рис. 1.4. Диаграмма Эйлера-Венна для симметрической разности

Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 1.5):

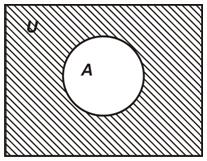
Рис. 1.5. Диаграмма Эйлера-Венна для абсолютного дополнения

Пример 5

С помощью диаграмм Эйлера-Венна докажем тождество:

.

Рассмотрим левую часть соотношения  и выполним действия по порядку:

1) найдем пересечение множеств В и С () (рис. 1.6, а);

2) найдем объединение полученного множества  с множеством А () (рис. 1.6, б).

Рассмотрим правую часть соотношения :

1) найдем объединение множеств А и В  (рис. 1.6, в);

2) найдем объединение множеств А и С  (рис. 1.6, г);

3) найдем пересечение двух последних множеств  и  () (рис. 6, д):

В обоих случаях (рис. 1.6, б) и (рис. 1.6, д) получаем равные множества. Следовательно, исходное соотношение справедливо.

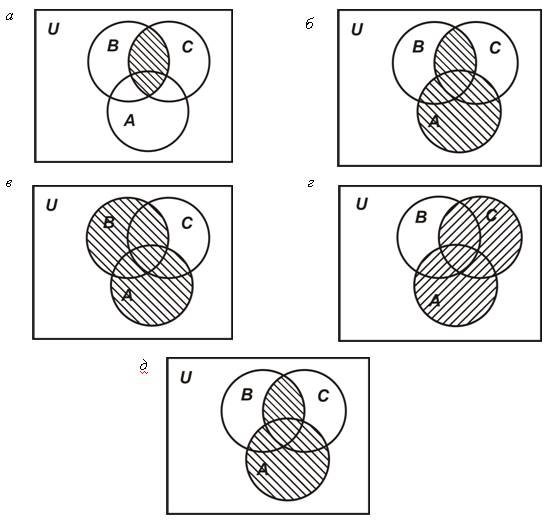
Рис. 1.6. Доказательство тождества с помощью диаграмм Эйлера-Венна

Рассмотрим основные тождества алгебры множеств. Для произвольных множеств А, В, и С справедливы следующие соотношения (табл. 1.11):

Таблица 1.11 Основные тождества алгебры множеств

Объединение	Пересечение
1. Коммутативность объединения	1′. Коммутативность пересечения
2. Ассоциативность объединения	2′. Ассоциативность пересечения
3. Дистрибутивность объединения относительно пересечения	3′. Дистрибутивность пересечения относительно объединения
4. Законы действия с пустым и универсальным множествами	4′. Законы действия с пустым и универсальным множествами
5. Закон идемпотентности объединения	5′. Закон идемпотентности пересечения
6. Закон де Моргана	6′. Закон де Моргана
7. Закон поглощения	7′. Закон поглощения
8. Закон склеивания	8′. Закон склеивания
9. Закон Порецкого	9′. Закон Порецкого
10. Закон двойного дополнения

Пример 6

Доказать следующее тождество:

.

Решение

Докажем это тождество двумя способами: аналитически (используя равносильности алгебры множеств) и графически (используя диаграммы Эйлера-Венна).

Используем равносильности алгебры множеств:

1) используя соотношение 3 (табл. 1.11),  получим:

;

2) используя соотношение 4 (табл. 1.11),  получим:

;

3) используя соотношение 4′ (табл. 1.11),  получим:

.

Построим соответствующие диаграммы Эйлера-Венна:

1) найдем  (рис. 1.7, а);

2) найдем  (рис. 1.7, б);

1) определим объединение множеств  и  (рис. 1.7, в).

Из рисунка (рис. 1.7, в) видно, что

.

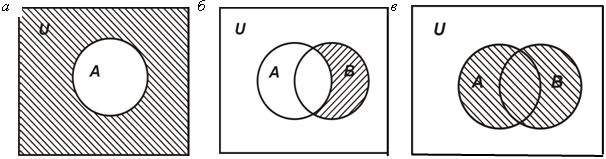
Рис. 1.7. Доказательство тождества с помощью диаграмм Эйлера-Венна

Определение. Упорядоченная пара <x, y> определяется как совокупность, состоящая из двух элементов х и у, расположенных в определенном порядке. Две пары <x, y>, <u, v> считаются равными тогда и только тогда, когда x = u, y = v.

Упорядоченная n-ка элементов х₁, …, х_n обозначается <x₁, …, x_n>.

Определение. Прямым произведением множеств X и Y называется множество , элементами которого являются все возможные упорядоченные пары <x, y>, такие, что .

Определение. Прямым произведением множеств Х₁, Х₂, …, Х_n называется совокупность всех упорядоченных n-ок <x₁, …, x_n> таких, что . Если Х₁=Х₂=…Х_n, то пишут .

Пример 7

1) Пусть X = {1, 2, 3}, Y = {0, 1}. Тогда

;

.

2) Пусть Х – множество точек отрезка [0, 1], а Y – множество точек отрезка [1, 2]. Тогда  – множество точек квадрата  с вершинами в точках (0, 1), (0, 2), (1, 1), (1,2).

Определение. Бинарным (или двуместным) отношением r называется множество упорядоченных пар.

Если r есть отношение и пара <x, y> принадлежит этому отношению, то наряду с записью <x, y>Îr употребляется запись xry. Элементы х и у называются координатами (или компонентами) отношения r.

Определение. N-арным отношением называется множество n  упорядоченных элементов.

Определение. Областью определения бинарного отношения r называется множество

Определение. Областью значений бинарного отношения r называется множество

Пример 8

Пусть отношение задано неравенством:

.

Тогда, например, пара чисел  не принадлежит отношению, так как

;

а пара  принадлежит отношению, так как

.